题目内容
19. 如图,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长等于( )
如图,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长等于( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 5$\sqrt{2}$ |
分析 在Rt△AOB中,已知了OB的长和∠A的度数,根据直角三角形的性质可求得OA的长,也就得到了直径AD的值,连接CD,同理可在Rt△ACD中求出AC的长,由BC=AC-AB即可得解.
解答  解:连接CD;
解:连接CD;
Rt△AOB中,∠A=30°,OB=5,则AB=10,OA=5$\sqrt{3}$;
在Rt△ACD中,∠A=30°,AD=2OA=10$\sqrt{3}$,
∴AC=cos30°×10$\sqrt{3}$=$\frac{\sqrt{3}}{2}$×10$\sqrt{3}$=15,
∴BC=AC-AB=15-10=5,
故选C.
点评 本题主要考查了直角三角形的性质和圆周角定理的应用,难度不大.

练习册系列答案
相关题目
11.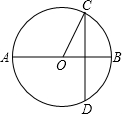 如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | π | D. | 2π |