题目内容
1.当x满足$\left\{\begin{array}{l}{2x<4x-4}\\{\frac{1}{3}(x-6)>\frac{1}{2}(x-6)}\end{array}\right.$时,方程x2-2x-5=0的根是( )| A. | 1±$\sqrt{6}$ | B. | $\sqrt{6}$-1 | C. | 1-$\sqrt{6}$ | D. | 1+$\sqrt{6}$ |
分析 先求出不等式组的解,再求出方程的解,根据范围即可确定x的值.
解答 解:$\left\{\begin{array}{l}{2x<4x-4}\\{\frac{1}{3}(x-6)>\frac{1}{2}(x-6)}\end{array}\right.$,
解得:2<x<6,
∵方程x2-2x-5=0,
∴x=1±$\sqrt{6}$,
∵2<x<6,
∴x=1+$\sqrt{6}$.
故选D.
点评 本题考查解一元一次不等式、一元二次方程的解等知识,熟练掌握不等式组以及一元二次方程的解法是解题的关键,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.计算2-2(1-a)的结果是( )
| A. | a | B. | -a | C. | 2a | D. | -2a |
9.据中国电子商务研究中心监测数据显示,2016年第二季度中国轻纺城市场群的商品成交额达29600 000 000元,将29600 000 000用科学记数法表示为( )
| A. | 2.96×1010 | B. | 2.96×1011 | C. | 29.6×1010 | D. | 0.296×1011 |
6.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则$\widehat{BC}$的度数是( )


| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
 如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )
如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )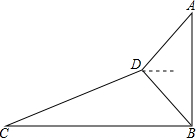 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)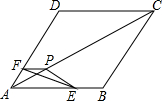 如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.