题目内容
16.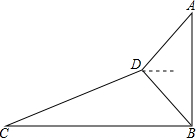 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)(1)求点D距水平面BC的高度为多少米;
(2)求大楼AB的高度约为多少米.
分析 (1)作DE⊥AB于E,作DF⊥BC于F,y由CD的坡度为i=1:2.4,CD=104米,得到$\frac{DF}{CF}$=1:2.4,根据勾股定理列方程,即可得到结论;
(2)根据矩形的性质得到BE=40m,由等腰直角三角形的性质得到DE=BE=40m,根据三角函数的定义即可得到结果.
解答 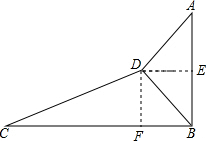 解:(1)作DE⊥AB于E,作DF⊥BC于F,
解:(1)作DE⊥AB于E,作DF⊥BC于F,
∵CD的坡度为i=1:2.4,CD=104米,
∴$\frac{DF}{CF}$=1:2.4,
∴$\sqrt{D{F}^{2}+(2.4DF)^{2}}$=104,
∴DF=40(米);
(2)∵DF=40m,
∴BE=40m,
∵∠BDE=45°,
∴DE=BE=40m,
在Rt△ADE中,∠ADE=37°,
∴AE=tan37°•40=30(米)
∴AB=AE+BE=70m.
点评 本题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
7.下列计算正确的是( )
| A. | a3+a4=a7 | B. | a3•a4=a7 | C. | a3-a4=a-1 | D. | a3÷a4=a |
1.当x满足$\left\{\begin{array}{l}{2x<4x-4}\\{\frac{1}{3}(x-6)>\frac{1}{2}(x-6)}\end{array}\right.$时,方程x2-2x-5=0的根是( )
| A. | 1±$\sqrt{6}$ | B. | $\sqrt{6}$-1 | C. | 1-$\sqrt{6}$ | D. | 1+$\sqrt{6}$ |
8.人类的遗传物质是DNA,DNA是很大的链,最短的22号染色体长达30000000个核苷酸,30000000用科学记数法表示为( )
| A. | 3×108 | B. | 3×107 | C. | 3×106 | D. | 0.3×108 |
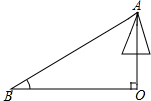 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为30tanα米(用三角函数表示)
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为30tanα米(用三角函数表示)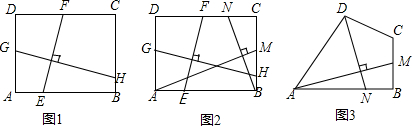
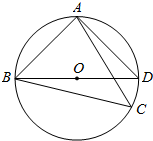 如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°
如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°