题目内容
如图①,在△ABC中∠ACB=90°,AC=BC,M是AB中点,P为AB上一动点(P不与A、B重合),PE⊥AC于点E,PF⊥BC于点F.
(1)求证:ME=MF,ME⊥MF;
(2)如点P移动至AB的延长线上,如图②,是否仍有如上结论?请予以证明.

(1)求证:ME=MF,ME⊥MF;
(2)如点P移动至AB的延长线上,如图②,是否仍有如上结论?请予以证明.

考点:全等三角形的判定与性质
专题:
分析:(1)连接CM,易证四边形CEFP是矩形,可得FP=CE,即可求得CE=PF=BF,即可证明△ECM≌△FBM,可得EM=FM,∠EMC=∠FMB,即可解题;
(2)连接CM,易证四边形CEP'F是矩形,可得P'F=CE,BF=FP',即可证明△CEM≌△BFM,可得ME=MF,∠CME=∠BMF,即可解题.
(2)连接CM,易证四边形CEP'F是矩形,可得P'F=CE,BF=FP',即可证明△CEM≌△BFM,可得ME=MF,∠CME=∠BMF,即可解题.
解答:证明:(1)连接CM,
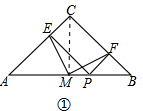
∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形CEFP是矩形,
∴FP=CE,
∵∠ACB=90°,AC=BC
∴∠ACM=∠B=45°,CM⊥AB,CM=BM,
∵PF⊥BC,
∴△BFP为等腰直角三角形,
∴PF=BF,
∴CE=PF=BF,
在△ECM和△FBM中,
,
∴△ECM≌△FBM(SAS),
∴EM=FM,∠EMC=∠FMB,
∵∠FMB+∠CMF=90°,
∴∠EMC+∠CMF=90°.即EM⊥FM;
(2)连接CM,
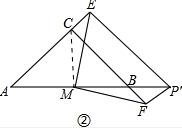
∵P'F⊥CF,P'E⊥CE,
∴四边形CEP'F是矩形,∴P'F=CE,
∵∠ACB=90°,AC=BC,
∴∠CBM=∠BCM=45°,BM=BM,CM⊥AB,
∴∠MBF=∠MCE=135°,∠FBP'=45°,
∴BF=FP',
在△CEM和△BFM中,
,
∴△CEM≌△BFM(SAS),
∴ME=MF,∠CME=∠BMF,
∵∠CMB+∠EMB=90°,
∴∠EMB+∠FMB=∠EMF=90°,即EM⊥FM.

∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形CEFP是矩形,
∴FP=CE,
∵∠ACB=90°,AC=BC
∴∠ACM=∠B=45°,CM⊥AB,CM=BM,
∵PF⊥BC,
∴△BFP为等腰直角三角形,
∴PF=BF,
∴CE=PF=BF,
在△ECM和△FBM中,
|
∴△ECM≌△FBM(SAS),
∴EM=FM,∠EMC=∠FMB,
∵∠FMB+∠CMF=90°,
∴∠EMC+∠CMF=90°.即EM⊥FM;
(2)连接CM,

∵P'F⊥CF,P'E⊥CE,
∴四边形CEP'F是矩形,∴P'F=CE,
∵∠ACB=90°,AC=BC,
∴∠CBM=∠BCM=45°,BM=BM,CM⊥AB,
∴∠MBF=∠MCE=135°,∠FBP'=45°,
∴BF=FP',
在△CEM和△BFM中,
|
∴△CEM≌△BFM(SAS),
∴ME=MF,∠CME=∠BMF,
∵∠CMB+∠EMB=90°,
∴∠EMB+∠FMB=∠EMF=90°,即EM⊥FM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CEM≌△BFM是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
以下列各组数据为三角形的三边长,能构成直角三角形的是( )
| A、2cm,3cm,4cm |
| B、3cm,5cm,6cm |
| C、2cm,6cm,40cm |
| D、6cm,8cm,10cm |
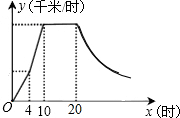 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题: 如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数.
如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数. 一质点P从距原点1个单位的A点处向原点方向跳动,第一次跳动到OA的中点A1处,第二次从A1点跳动到OA1的中点A2处,第三次从A2点跳动到OA2的中点A3处,如此不断跳动下去,则第5次跳动后,该质点到原点O的距离为
一质点P从距原点1个单位的A点处向原点方向跳动,第一次跳动到OA的中点A1处,第二次从A1点跳动到OA1的中点A2处,第三次从A2点跳动到OA2的中点A3处,如此不断跳动下去,则第5次跳动后,该质点到原点O的距离为 如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.
如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.