题目内容
10．
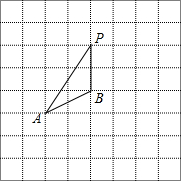如图，将△ABP放在每个小正方形的边长为1的网格中，点A、B、P均落在格点上．（1）△ABP的面积等于2；
（2）若线段AB水平移动到A′B′，且使PA′+PB′最短，请你在如图所示的网格中，用直尺画出A′B′，并简要说明画图的方法（不要求证明）$\sqrt{5}$．
分析 （1）直接根据三角形的面积公式即可得出结论；
（2）将点A向下平移2格得到点Q，连接PQ，与点A所在的水平线交于点A′，同时将点PQ向上平移1格，再向右平移2格得到点M、N，连接MN与点B所在水平线交于点B′，连接A′B′即为所求．
解答 解：（1）S△ABC=$\frac{1}{2}$×2×2=2．
故答案为：2；
（2）如图所示，A′B′=AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$．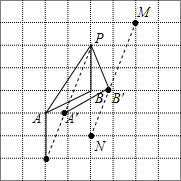
故答案为：$\sqrt{5}$．
点评 本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
20．
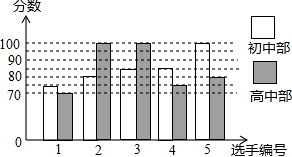某中学举行歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
求得初中代表队选手决赛成绩的平均数和方差：
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85，
${{S}_{1}}^{2}$=$\frac{1}{5}$[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70；
（1）根据图示填写表格：
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
某中学举行歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．求得初中代表队选手决赛成绩的平均数和方差：
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85，
${{S}_{1}}^{2}$=$\frac{1}{5}$[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70；
（1）根据图示填写表格：
| 平均数（分） | 中位数（分） | 众数（分） | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
（3）计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
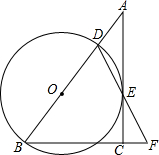在Rt△ABC中，∠ACB=90°，D是AB边上的一点，以BD为直径作⊙O．与AC相切于点E，连结DE并延长与BC的延长线交于点F．
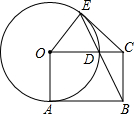如图所示，在矩形OABC中，以O为圆心，OA为半径作圆，交OC，于点D，连接BD并延长，交⊙O于点E，连接OE，EC，EC=BC．
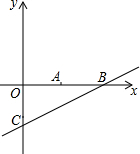在平面直角坐标系xOy中，点A、点B、点C坐标分别为（5，0）、（10，0）、（0，-5）．