题目内容
2.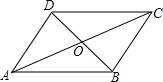 已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
分析 由四边形ABCD是平行四边形,即可得AB=CD,AD=BC,OA=OC,然后由平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长多8cm,可得AB-BC=8cm,2(AB+BC)=60cm,继而可求得AB的长,即可得CD的长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵△AOB的周长比△BOC的周长多8cm,
∴(OA+OB+AB)-(OB+OC+BC)=8cm,
即AB-BC=8cm,①
∵平行四边形ABCD的周长为60cm,
∴2(AB+BC)=60cm,②
∴由①②得到:AB=19cm,BC=11cm.
点评 此题考查了平行四边形的性质.此题难度不大,注意掌握平行四边形对边相等与对角线互相平分的定理的应用,注意数形结合思想与方程思想的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
10.一辆汽车以平均每小时x千米的速度上坡,到达某地后立刻以平均每小时y千米的速度返回,则全程中这辆汽车的平均速度是( )
| A. | $\frac{x+y}{xy}$ | B. | $\frac{x+y}{2}$ | C. | $\frac{xy}{x+y}$ | D. | $\frac{2xy}{x+y}$ |
11.到三角形三边的距离相等的点P应是三角形的三条( )的交点.
| A. | 角平分线 | B. | 高 | C. | 中线 | D. | 垂直平分线 |
12. 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 125° | D. | 135° |
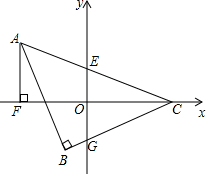 如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.
如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.