题目内容
12. 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 125° | D. | 135° |
分析 根据垂直的定义得到∠EBC=∠EDC=90°,根据四边形的内角和得到∠C=360°-∠CBE-∠CDE-∠E=125°,根据平行四边形的性质得到∠A=∠C=125°,
解答 解:∵EB⊥BC于B,ED⊥CD于D,
∴∠EBC=∠EDC=90°,
∵∠E=55°,
∴∠C=360°-∠CBE-∠CDE-∠E=125°,
∵四边形ABCD为平行四边形,
∴∠A=∠C=125°,
故选C.
点评 本题考查了平行四边形的性质,垂直的定义,四边形的内角和,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
相关题目
1.抛物线y=$\frac{1}{2}$x2向下平移一个单位得到抛物线( )
| A. | y=$\frac{1}{2}$(x+1)2 | B. | y=$\frac{1}{2}$(x-1)2 | C. | y=$\frac{1}{2}$x2+1 | D. | y=$\frac{1}{2}$x2-1 |
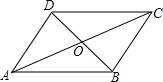 已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.