题目内容
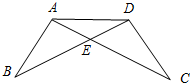 在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
(1)上述三个条件中,由哪两个条件可以判定△AED是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
考点:等腰三角形的判定与性质
专题:开放型
分析:(1)只要能证明△ABE≌△DCE的条件都可以,所以可以根据全等三角形的判定方法来写出答案;
(2)选择一种证明△ABE≌△DCE,可得到AE=DE,可证明△AED为等腰三角形.
(2)选择一种证明△ABE≌△DCE,可得到AE=DE,可证明△AED为等腰三角形.
解答:解:(1)①③、①④、②③、②④都可以证明△ABE≌△DCE,可得到AE=DE,可判定△AED为等腰三角形;
(2)选择①③,证明如下:
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,
∴△AED为等腰三角形.
(2)选择①③,证明如下:
在△ABE和△DCE中,
|
∴△ABE≌△DCE(AAS),
∴AE=DE,
∴△AED为等腰三角形.
点评:本题主要考查等腰三角形的判定,掌握等角对等边是解题的关键,注意全等三角形的性质的应用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
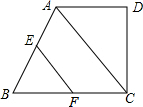 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值.
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=CD,点E,F分别是AB,BD的中点,若EF=2,求CD的值. 如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.
如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.
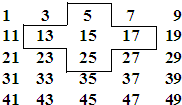 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.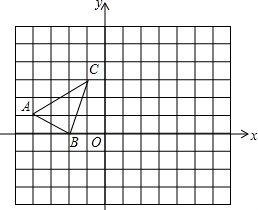 如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,0),点C的坐标为(-1,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,0),点C的坐标为(-1,3).