题目内容
2.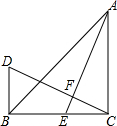 在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
分析 根据题意得到一对直角相等,再由公共角,得到三角形ECF与三角形ACE相似,利用相似三角形对应角相等得到一对角相等,再由一对直角相等,夹边BC=AC,利用ASA得到三角形DCB与三角形ACE全等,利用全等三角形对应边相等即可得证.
解答 证明:∵AE⊥CD,
∴∠CFE=∠ACE=90°,
∵∠FEC=∠CEA,
∴△CEF∽△AEC,
∴∠EAC=∠DCB,
在△CBD和△ACE中,
$\left\{\begin{array}{l}{∠DCB=∠EAC}\\{BC=AC}\\{∠DBC=∠ECA=90°}\end{array}\right.$,
∴△CBD≌△ACE(ASA),
则AE=CD.
点评 此题考查了全等三角形的判定与性质,构造全等三角形是解本题的关键.

练习册系列答案
相关题目
11.设函数y=x+5与$y=\frac{3}{x}$的图象的两个交点的横坐标为a、b,则$\frac{1}{a}+\frac{1}{b}$的值是( )
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
11.已知点A的坐标为(-2,3),点B的坐标为(0,1),则点A关于点B对称点的坐标为( )
| A. | (-2,2) | B. | (2,-3) | C. | (2,-1) | D. | (2,3) |
12.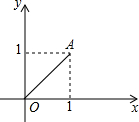 如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
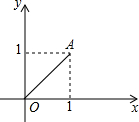 如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )| A. | (-$\sqrt{2}$,0) | B. | (0,-$\sqrt{2}$) | C. | (0,-1) | D. | (-1,0) |
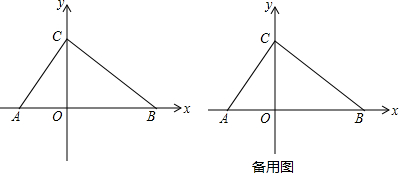
 如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.
如图,已知△ABC和点O,画出与△ABC关于点O对称的△A′B′C′.