题目内容
17.在△ABC中,AB=AC,∠BAC=90°,D是BC上任意一点.(1)读语句画图(保留作图痕迹,不写画法):
①把△ABD沿着AD对折,得到△ADF,画出对折后的△ADF;
②翻折AC,使AC与AF叠合,折痕与BC交于点E,画出折痕AE,连接EF;
(2)翻折后点C与点F是否重合?猜想△DEF是什么三角形?
(3)证明你的结论.
分析 (1)根据题意画出图形,如图所示;
(2)翻折后点C与点F能重合,猜想△DEF是直角三角形;
(3)由折叠的性质得到两对角相等,根据直角三角形两锐角互余,等量代换即可得证.
解答 解:(1)根据题意画出相应的图形,如图所示:
(2)C与F能重合,猜想△DEF为直角三角形;
(3)证明:由折叠可得∠AFD=∠B,∠AFE=∠C,
∵∠B+∠C=90°,
∴∠AFD+∠AFE=90°,
则△DEF为直角三角形.
点评 此题考查了翻折变换,作图,以及翻折的性质,熟练掌握翻折的性质是解本题的关键.

练习册系列答案
相关题目
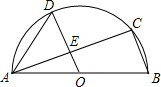 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.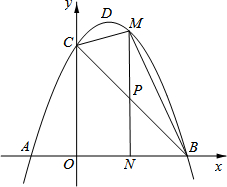 如图,抛物线y=-x2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.
如图,抛物线y=-x2+bx+c的顶点为D,与x轴交于A(-1,0)、B(3,0),与y轴交于点C.
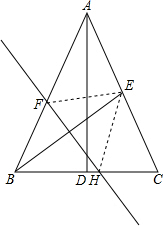 如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.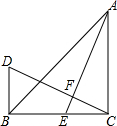 在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
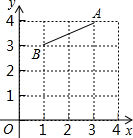 如图,在平面直角坐标系中,将线段AB绕点B按顺时针方向旋转90°后,得到线段A′B,则点A′的坐标为(2,1).
如图,在平面直角坐标系中,将线段AB绕点B按顺时针方向旋转90°后,得到线段A′B,则点A′的坐标为(2,1).