题目内容
10.菱形ABCD中,E为对角线BD上一点,过点E作BD的垂线交直线AB于点P,连接PC交BD于点F,若AC=4,BD=8,tan∠EPF=$\frac{1}{2}$,则EF的长为$\frac{3}{5}$.分析 由菱形的性质和已知条件得出∠ABO=∠EPF,证明△PEF∽△COF,得出∠EPF=∠COF,由tan∠EPF=tan∠OCF=$\frac{OF}{OC}$=$\frac{1}{2}$,求出OF=1,BF=3,设EF=x,则PE=2x,由tan∠ABO=$\frac{PE}{BE}$=$\frac{1}{2}$,得出BE=2PE=4x,得出BF=BE+EF=5x=3,解方程求出x即可.
解答 解:如图所示: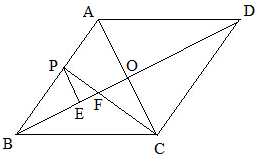 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=2,OB=OD=$\frac{1}{2}$BD=4,
∴tan∠ABO=$\frac{OA}{OB}$=$\frac{2}{4}$=$\frac{1}{2}$=tan∠EPF,
∴∠ABO=∠EPF,
∵PE⊥BD,
∴PE∥AC,
∴△PEF∽△COF,
∴∠EPF=∠COF,
∴tan∠EPF=tan∠OCF=$\frac{OF}{OC}$=$\frac{1}{2}$,
∴OF=1,BF=3.
设EF=x,则PE=2x,
∵PE⊥BD,
∴tan∠ABO=$\frac{PE}{BE}$=$\frac{1}{2}$,
∴BE=2PE=4x,
∴BF=BE+EF=5x=3,
解得:x=$\frac{3}{5}$,
即EF=$\frac{3}{5}$.故答案为:$\frac{3}{5}$.
点评 本题考查了菱形的性质、相似三角形的判定与性质以及三角函数;本题有一定难度,需要通过证明三角形相似,运用三角函数列出方程才能得出结果.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.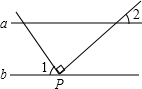 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
 如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )
如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为( )| A. | 24° | B. | 34° | C. | 44° | D. | 54° |
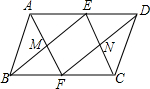 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )
已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )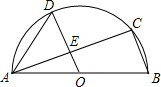 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.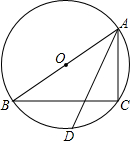 如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.
如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=60°,弦AD平分∠BAC,若AD=6,那么AC=$2\sqrt{3}$.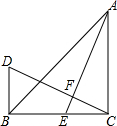 在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.
在△ABC中,∠ACB=90°,AC=BC,CD⊥AE于点F,BD⊥BC于点B,AE为BC边上的中线,试说明:AE=CD.