题目内容
5. 如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.
如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.(1)试判断AF与CF的位置关系,并证明;
(2)若AB=4.
①求DF的长;
②连接OF,交AD于点M,求DM的长.
分析 (1)AF⊥CF,连接OD,由CD是⊙O的切线,得到OD⊥CD,根据等腰三角形的性质得到∠DAF=∠CAD,于是求得∠FAD=∠ODA,推出AF∥OD,结论即可得出;
(2)①如图,连接OD,由CF是⊙O的切线,得到OD⊥CF,根据AB为⊙O的直径,AB=4,求得半径OD=OB=$\frac{1}{2}$AB=2,得到BC=3,根据射影定理和勾股定理得到CD=$\sqrt{21}$,CE=$\frac{21}{5}$,通过△CED∽△CFA,得到CF=$\frac{7\sqrt{21}}{5}$,②通过勾股定理和三角形相似即可解出结果.
解答 解:(1)AF⊥CF,
证明;连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,
∵OA=OD,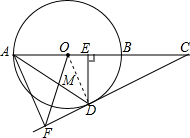
∴∠CAD=∠ODA,
∵∠DAF=∠CAD,
∴∠FAD=∠ODA,
∴AF∥OD,
∴AF⊥CF;
(2)①如图,连接OD,
∵CF是⊙O的切线,
∴OD⊥CF,
∵AB为⊙O的直径,AB=4,
∴OD=OB=$\frac{1}{2}$AB=2,
∵2BC=3OB,
∴BC=3,
∵DE⊥AC,
∴CD2=CE•CO=OC2-OD2=52-22,
∴CD=$\sqrt{21}$,CE=$\frac{21}{5}$,
∵∠AFC=∠CED=90°,∠C=∠C,
∴△CED∽△CFA,
∴$\frac{CD}{AC}=\frac{CE}{CF}$,即$\frac{\sqrt{21}}{7}=\frac{\frac{21}{5}}{CF}$,
∴CF=$\frac{7\sqrt{21}}{5}$,
②∵CF=$\frac{7\sqrt{21}}{5}$,CD=$\sqrt{21}$,
∴DF=CF-CD=$\frac{2\sqrt{21}}{5}$;
∵∠DAF=∠CAD,DF⊥AF,DE⊥AE,
∴DE=DF=$\frac{2\sqrt{21}}{5}$,
∵AE=AC-CE=$\frac{14}{5}$,
∴AD=$\sqrt{{AE}^{2}+D{E}^{2}}$=$\frac{2\sqrt{70}}{5}$,
∵AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=$\frac{14}{5}$
∵OD∥AF,
∴△OMD∽△AMF,
∴$\frac{OD}{AF}=\frac{DM}{AM}$,即$\frac{2}{\frac{14}{5}}=\frac{DM}{\frac{2\sqrt{70}}{5}-DM}$,
解得:DM=$\frac{\sqrt{70}}{6}$.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,射影定理,角平分线的性质,正确的识别图形是解题的关键.

| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| 工种 属地 | 钳工 | 车工 |
| A地 | 1800(元/月) | 1600(元/月) |
| B地 | 1600(元/月) | 1200(元/月) |
(1)派往B地20-x名钳工,派往B地15+x名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
 如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.
如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$. (1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
(1)计算:$\sqrt{8}$-(π-1)0-4sin45°;