题目内容
17.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
分析 (1)经销商能盈利=水果箱数×每箱水果的盈利;
(2)设甲店配A种水果x箱,分别表示出配给乙店的A水果,B水果的箱数,根据盈利不小于110元,列不等式求解,进一步利用经销商盈利=A种水果甲店盈利×x+B种水果甲店盈利×(10-x)+A种水果乙店盈利×(10-x)+B种水果乙店盈利×x;列出函数解析式利用函数性质求得答案即可.
解答 解:(1)经销商能盈利=5×11+5×17+5×9+5×13=5×50=250;
(2)设甲店配A种水果x箱,则甲店配B种水果(10-x)箱,
乙店配A种水果(10-x)箱,乙店配B种水果10-(10-x)=x箱.
∵9×(10-x)+13x≥100,
∴x≥2$\frac{1}{2}$,
经销商盈利为w=11x+17•(10-x)+9•(10-x)+13x=-2x+260.
∵-2<0,
∴w随x增大而减小,
∴当x=3时,w值最大.
甲店配A种水果3箱,B种水果7箱.乙店配A种水果7箱,B种水果3箱.最大盈利:-2×3+260=254(元).
点评 此题考查一元一次不等式的运用,一次函数的实际运用,找出题目蕴含的不等关系与等量关系解决问题.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
7.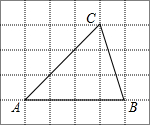 如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
 如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | 2 | D. | $\frac{5}{2}$ |
5.二次函数y=x2+4x-5的图象的对称轴为( )
| A. | x=4 | B. | x=-4 | C. | x=2 | D. | x=-2 |
10.已知x=-1是关于x的方程x2-x+m=0的一个根,则m的值为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |

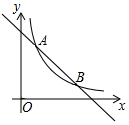 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点. 如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.
如图,AB为⊙O的直径,延长AB到点C,使得2BC=3OB,过点C作⊙O的切线,交⊙O于点D,过点D作DE⊥AC,连接AD,作∠DAF=∠CAD,交CD的延长线于点F.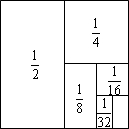 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.