Question

8．如图，在平面直角坐标系xOy中，直径为10的⊙E交x轴于点A（-2，0）、B（4，0），交y轴于点C、D，试求圆心E和点C、D的坐标．

Answer 1

分析 过E作OF⊥AB于F，连接OE、EC，先根据A、B点的坐标求出AB的长，再根据垂径定理求出BF的长，OF的长即可求出，再利用勾股定理求出弦心距，E点坐标也就求出了，进而CD的弦心距也就可以得到，再利用勾股定理即可求出弦CD的一半的长，即可求出C、D两点坐标．

解答 解：作EF⊥x轴，交x轴于点F，连接EB，
∵A、B的坐标分别为（-2，0）、（4，0），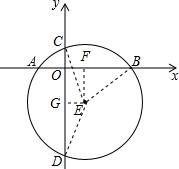
∴AB=6，OB=4，
∴BF=3，
∴OF=1，
∵⊙E的直径为10，
∴半径EB=5，
∴EF=4，
∴E的坐标是（1，-4）．
作EG⊥y轴，交y轴于点G，连接EC、ED，
由勾股定理CG=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$，
∴点C的坐标是（0，2$\sqrt{6}$-4），
点D的坐标是（0，-4-2$\sqrt{6}$）．

点评 本题主要考查垂径定理的应用和勾股定理的运用，熟练掌握定理是解题的关键．