题目内容
20. 如图,已知OP平分∠AOB,过点P作OP的垂线分别交OA、OB于点C、D,请问:PC=PD吗?为什么?能不能利用角平分线的性质求证呢?
如图,已知OP平分∠AOB,过点P作OP的垂线分别交OA、OB于点C、D,请问:PC=PD吗?为什么?能不能利用角平分线的性质求证呢?
分析 作PE⊥OC于E,PF⊥OD于F,根据直角三角形的性质得到∠EPC=∠FPD,根据角平分线的性质得到PE=PF,证明△EPC≌△FPD即可.
解答  解:PC=PD,
解:PC=PD,
作PE⊥OC于E,PF⊥OD于F,
∵OP⊥CD,
∴∠EPC=∠FPD,
∵OP平分∠AOB,PE⊥OC,PF⊥OD,
∴PE=PF,
在△EPC和△FPD中,
$\left\{\begin{array}{l}{∠EPC=∠FPD}\\{PE=PF}\\{∠PEC=∠PFD}\end{array}\right.$,
∴△EPC≌△FPD,
∴PC=PD.
点评 本题考查的是角平分线的性质和全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A(-2,0)、B(4,0),交y轴于点C、D,试求圆心E和点C、D的坐标.
如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A(-2,0)、B(4,0),交y轴于点C、D,试求圆心E和点C、D的坐标.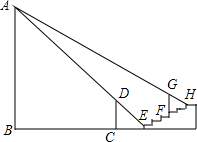 如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高.
如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高. 如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.
如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.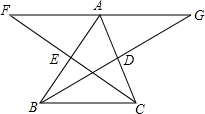 已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF
已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF 如图,焊上等长的13根钢条来加固钢架,AP1=P1P2=P2P3=…=P13P14=P13A,则∠A的度数是12°.
如图,焊上等长的13根钢条来加固钢架,AP1=P1P2=P2P3=…=P13P14=P13A,则∠A的度数是12°.