题目内容
17．
如图所示，在△ABC中，∠A=36°，且∠ABC=∠C，BD是△ABC的高．试求∠C与∠DBC的度数．
分析 首先根据三角形的内角和定理，用180°减去∠A的度数，求出∠ABC与∠C的度数和是多少；然后用∠ABC与∠C的度数和除以2，求出∠C的度数是多少；最后在△BCD中，根据三角形的内角和定理，求出∠DBC的度数是多少即可．
解答 解：∵∠A=36°，
∴∠ABC+∠C=180°-36°=144°，
又∵∠ABC=∠C，
∴∠C=144°÷2=72°．
∵BD是△ABC的高，
∴∠BDC=90°，
∴∠DBC=180°-90°-72°=18°．
点评 此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，直径为10的⊙E交x轴于点A（-2，0）、B（4，0），交y轴于点C、D，试求圆心E和点C、D的坐标．
如图，∠ABC的平分线与∠ACB的外角平分线相交于点D，连接AD．求证：AD是∠BAC的外角平分线．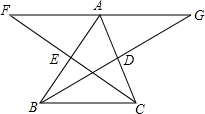
已知：如图，BD、CE为△ABC的两条中线，延长BD到G，使BD=DG，延长CE到F，使CE=EF
如图，AC=BD，BC=AD，求证：∠1=∠2．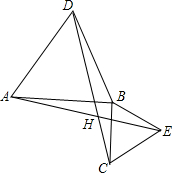
如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：