题目内容
3. 已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.
已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.(1)求两个函数的解析式;
(2)求△AOB的面积.
分析 (1)首先把点B(-2,4)代入二次函数y=ax2得出a,再把点A(1,m)代入二次函数解析式得出m,进一步把A、B代入一次函数y=kx+b求得一次函数即可;
(2)利用一次函数求得点C坐标,把△AOB的面积分为△AOC与△COB的面积和即可.
解答 解:(1)把点B(-2,4)代入二次函数y=ax2得4a=4,a=1,
二次函数的解析式y=x2;
点A(1,m)代入二次函数解析式得m=1,
把点A(1,1),B(-2,4)代入一次函数y=kx+b得
$\left\{\begin{array}{l}{k+b=1}\\{-2k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
故一次函数的解析式y=-x+2.
(2)一次函数与y轴交于点C(0,2),
S△AOB=S△AOC+S△COB=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3.
点评 此题考查待定系数法求求一次函数、二次函数解析式,三角形的面积,正确利用函数图象上的点解决问题.

练习册系列答案
相关题目
18. 一个飞镖盘由两个同心圆组成,两圆的半径之比为1:2,任意投掷一个飞镖,击中B区的概率是击中A区概率的( )
一个飞镖盘由两个同心圆组成,两圆的半径之比为1:2,任意投掷一个飞镖,击中B区的概率是击中A区概率的( )
 一个飞镖盘由两个同心圆组成,两圆的半径之比为1:2,任意投掷一个飞镖,击中B区的概率是击中A区概率的( )
一个飞镖盘由两个同心圆组成,两圆的半径之比为1:2,任意投掷一个飞镖,击中B区的概率是击中A区概率的( )| A. | 2倍 | B. | 3倍 | C. | 4倍 | D. | 6倍 |
 如图,AB是⊙O的直径,CD是弦,且CD⊥AB,垂足是P.如果CD=4,PB=1,那么直径AB=5.
如图,AB是⊙O的直径,CD是弦,且CD⊥AB,垂足是P.如果CD=4,PB=1,那么直径AB=5. 如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A(-2,0)、B(4,0),交y轴于点C、D,试求圆心E和点C、D的坐标.
如图,在平面直角坐标系xOy中,直径为10的⊙E交x轴于点A(-2,0)、B(4,0),交y轴于点C、D,试求圆心E和点C、D的坐标.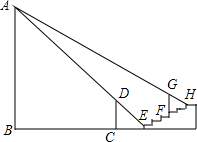 如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高.
如图,水平地面上竖立着一盏明亮的路灯A,AB垂直地面BC于B.旁边有6级台阶.每级台阶高0.2米,宽0.4米,现有身高1.4米的小明垂直站立在离第一级台阶1.2米的C处时.小明的影子刚好落在第一级台阶的边缘E处.身高0.9米的小华垂直站立在第四级台阶的边缘F处.其影子刚好落在第六级台阶的边缘H处.求路灯AB的高.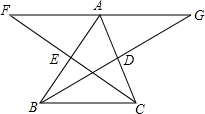 已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF
已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF