Question

13．如图，在四边形ABCD中，∠A=∠C=90°．
（1）求证：∠ABC+∠ADC=180°；
（2）作∠ABC的平分线BE交AD于点E，作DF∥BE于点F，求证：DF平分∠ADC．

Answer 1

分析 （1）根据四边形的内角和即可证明；
（2）根据平行线的性质可得∠2=∠DFC，然后根据（1）的结论和△DCF中利用内角和定理即可证得．

解答 证明：（1）∵四边形ABCD中，∠A+∠ABC+∠C+∠ADC=360°，∠A=∠C=90°，
∴∠ABC+∠ADC=180°，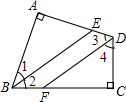
（2）∵DF∥BE，
∴∠2=∠DFC，
∵∠1=∠2，直角△DCF中，∠DFC+∠4=90°，
∴$\frac{1}{2}$∠ABC+∠4=90°，
∵∠ABC+∠ADC=180°，
即$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ADC=90°，
∴$\frac{1}{2}$∠ADC=∠4，
∴∠3=∠4，即DF平分∠ADC．

点评 本题考查了三角形和四边形的内角和定理，正确证明$\frac{1}{2}$∠ABC+∠4=90°是关键．