题目内容
16．
已知圆的半径是2$\sqrt{3}$，则该圆的内接正六边形的面积是（ ）| A． | 3$\sqrt{3}$ | B． | 9$\sqrt{3}$ | C． | 18$\sqrt{3}$ | D． | 36$\sqrt{3}$ |
分析 根据正六边形被它的半径分成六个全等的等边三角形，再根据等边三角形的边长，求出等边三角形的高，再根据面积公式即可得出答案．
解答 
解：连接OA、OB，作OG⊥AB于G，
∵等边三角形的边长是2$\sqrt{3}$，
∴高为3，
∴等边三角形的面积是3$\sqrt{3}$，
∴正六边形的面积是：18$\sqrt{3}$；
故选C．
点评 本题考查了正多边形和圆，解题的关键要记住正六边形的特点，它被半径分成六个全等的等边三角形．
练习册系列答案
寒假学与练系列答案
相关题目
6．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c=0无实数根；③a-b+c≥0；④$\frac{a+b+c}{b-a}$的最小值为3，其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
由许多小正方体堆积成一个几何体，其主视图、左视图如图所示，堆这样的几何体，至少需用6块小正方体，最多需用11块小正方体．
1．在同一平面内有三条直线，如果有且只有两条直线互相平行，那么这三条直线的交点个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
6．
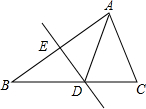如图所示．将△ABC沿直线DE折叠后，使点B与点A重合，已知AC=4cm，△ADC的周长为11cm，则BC的长为（ ）
如图所示．将△ABC沿直线DE折叠后，使点B与点A重合，已知AC=4cm，△ADC的周长为11cm，则BC的长为（ ）| A． | 11cm | B． | 15cm | C． | 7cm | D． | 10cm |