题目内容
3．一个直角三角形的斜边长比一条直角边长多2cm，另一条直角边长6cm，那么这个直角三角形的斜边长为（ ）| A． | 4cm | B． | 8cm | C． | 10cm | D． | 12cm |
分析 设直角三角形的斜边是xcm，则另一条直角边是（x-2）cm．根据勾股定理列方程求解即可．
解答 解：设直角三角形的斜边是xcm，则另一条直角边是（x-2）cm．
根据勾股定理，得
（x-2）2+36=x2，
解得：x=10．
则斜边的长是10cm．
故选C．
点评 本题考查了勾股定理的运用，解题的关键是根据勾股定理列出方程，熟练求得方程的解．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14．下列各组数是三角形的三边，能组成直角三角形的一组数是（ ）
| A． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ | B． | 2，3，4 | C． | 3，4，5 | D． | 6，8，12 |
如图，△ABC的三个顶点分别为A（1，1）、B（4，2）、C（3，4）．
18．
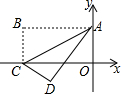如图，已知矩形纸片OABC在平面直角坐标系中，将该纸片沿对角线AC进行折叠，使得点B到达点D的位置，若该纸片的长为4、宽为2，则点D的坐标为（ ）
如图，已知矩形纸片OABC在平面直角坐标系中，将该纸片沿对角线AC进行折叠，使得点B到达点D的位置，若该纸片的长为4、宽为2，则点D的坐标为（ ）| A． | （-$\frac{12}{5}$，-$\frac{6}{5}$） | B． | （-$\frac{12}{5}$，-$\frac{8}{5}$） | C． | （$\frac{12}{5}$，-$\frac{6}{5}$） | D． | （$\frac{12}{5}$，-$\frac{8}{5}$） |
8．两会期间，记者随机抽取参会的部分代表，对他们某天发言的次数进行了统计，其结果如表，并绘制了如图所示的两幅不完整的统计图，请结合图中相关数据回答下列问题：
（1）求得样本容量为50，并补全直方图；
（2）如果会议期间组织1700名代表参会，请估计在这一天里发言次数不少于12次的人数；
（3）已知A组发表提议的代表中恰有1为女士，E组发表提议的代表中只有2位男士，现从A组与E组中分别抽一位代表写报告，请用列表法或画树状图的方法，求所抽的两位代表恰好都是男士的概率．
| 发言次数n | |
| A | 0≤n＜3 |
| B | 3≤n＜6 |
| C | 6≤n＜9 |
| D | 9≤n＜12 |
| E | 12≤n＜15 |
| F | 15≤n＜18 |
（2）如果会议期间组织1700名代表参会，请估计在这一天里发言次数不少于12次的人数；
（3）已知A组发表提议的代表中恰有1为女士，E组发表提议的代表中只有2位男士，现从A组与E组中分别抽一位代表写报告，请用列表法或画树状图的方法，求所抽的两位代表恰好都是男士的概率．
如图，已知BC∥DE，∠ABC=120°，那么直线AB、DE的夹角是120°或60°．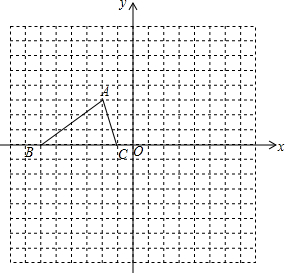
如图，已知△ABC的三个顶点坐标为A（-2，3），B（-6，0），C（-1，0）．