题目内容
11.计算:(1)$\sqrt{\frac{49}{2}}$+$\sqrt{108}-\sqrt{12}$
(2)($\sqrt{2}+\sqrt{6}$)2-$\sqrt{18}+\sqrt{\frac{1}{3}}+\frac{1}{5}\sqrt{50}$
(3)$\frac{\sqrt{72}-\sqrt{16}}{\sqrt{8}}-$($\sqrt{2}+\sqrt{3}$)($\sqrt{3}-\sqrt{2}$)
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先根据完全平方公式计算,再把各二次根式化为最简二次根式,然后合并即可;
(3)先进行二次根式的除法运算,再利用平方差公式计算,然后合并即可.
解答 解:(1)原式=$\frac{7\sqrt{2}}{2}$+6$\sqrt{3}$-2$\sqrt{3}$
=$\frac{7\sqrt{2}}{2}$+4$\sqrt{3}$;
(2)原式=2+4$\sqrt{3}$+6-3$\sqrt{2}$+$\frac{\sqrt{3}}{3}$+$\sqrt{2}$
=8+$\frac{13\sqrt{3}}{3}$-2$\sqrt{2}$;
(3)原式=$\sqrt{\frac{72}{8}}$-$\sqrt{\frac{16}{8}}$-(3-2)
=3-$\sqrt{2}$-1
=2-$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
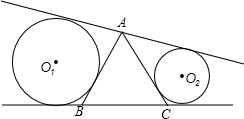 如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.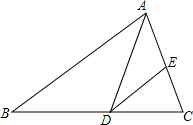 如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由.
如图,在△ABC中,AD是∠BAC的平分线,过D作DE∥AB,△AED是等腰三角形吗?说明理由. 如图,有两条长为10cm的纸带重叠摆放在一起(重叠部分为B).若A,B,C三部分的面积之比为3:2:3.则重叠部分B纸带的长度为4cm.
如图,有两条长为10cm的纸带重叠摆放在一起(重叠部分为B).若A,B,C三部分的面积之比为3:2:3.则重叠部分B纸带的长度为4cm.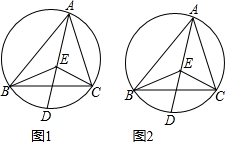
 如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3.
如图,梯形ABCD中,DC∥EF∥AB,DE=4,AE=6,BC=5,则BF=3. 如图所示一块长为20cm,宽10cm的矩形方框,镶在其外围的木质边框宽2cm,边框的内外边缘所成的矩形相似吗?为什么?
如图所示一块长为20cm,宽10cm的矩形方框,镶在其外围的木质边框宽2cm,边框的内外边缘所成的矩形相似吗?为什么?