题目内容
16.如图,△ABC是圆的内接三角形,点E为∠ABC和∠ACB的角平分线的交点,AE的延长线交圆于点D.(1)求证:$\widehat{BD}=\widehat{CD}$;
(2)判断B、E、C三点是否在以D为圆心,DE长为半径的⊙D上?并说明理由;
(3)如图2,若∠BEC=110°,则∠BDC=140°(直接写出结果).
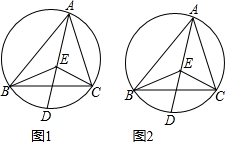
分析 (1)根据角平分线的性质求得AE是∠BAC的平分线,得出∠1=∠2,根据圆周角定理即可证得$\widehat{BD}=\widehat{CD}$;
(2)利用等弧所对的圆周角相等,可得∠BAD=∠CBD,再根据等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以B,E,C三点在以D为圆心,以DB为半径的圆上.
(3)根据圆周角定理求得∠BAC=55°,然后根据圆内接四边形的性质即可求得∠BDC的度数.
解答  解:(1)如图1,∵点E为∠ABC和∠ACB的角平分线的交点,
解:(1)如图1,∵点E为∠ABC和∠ACB的角平分线的交点,
∴AE是∠BAC的平分线,
∴∠1=∠2,
∴$\widehat{BD}=\widehat{CD}$;
(2)如图1,B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:∵∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴∠DBE=∠3+∠4,∠DEB=∠1+∠5,
∵BE是∠ABC的平分线,
∴∠4=∠5,
∴∠DBE=∠DEB,
∴DB=DE.
∵$\widehat{BD}=\widehat{CD}$,
∴BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.
(3)如图2,∵B,E,C三点在以D为圆心,以DB为半径的圆上,∠BEC=110°,
∵220°+∠BDC=360°,
∴∠BDC=140°.
故答案为140°.
点评 本题考查了圆周角定理和圆心角、弧、弦的关系,圆内接四边形的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
5. 将图中的角用不同方法表示出来,并填写下表:
将图中的角用不同方法表示出来,并填写下表:
 将图中的角用不同方法表示出来,并填写下表:
将图中的角用不同方法表示出来,并填写下表:| ∠1 | ∠3 | ∠3 | ∠4 | ∠5 |
| ∠BCE | ∠BAC | ∠BAE、∠BAC | ∠DAB | ∠ABC |
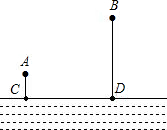 如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
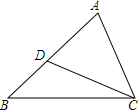 如图,∠B=∠ACD,S△ABC:S△ACD=2:1,则AC:AB=$\frac{\sqrt{2}}{2}$.
如图,∠B=∠ACD,S△ABC:S△ACD=2:1,则AC:AB=$\frac{\sqrt{2}}{2}$. 如图中等腰直角三角形ABC的腰为10厘米,阴影部分甲与乙的面积相等,求扇形AEF的面积.
如图中等腰直角三角形ABC的腰为10厘米,阴影部分甲与乙的面积相等,求扇形AEF的面积.