题目内容
 在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,
在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,求证:OC=FC.
考点:等腰三角形的判定
专题:证明题
分析:根据直角三角形的两锐角互余以及对顶角的性质,证明∠AFC=∠FOC,利用等角对等边即可证得.
解答:证明:∵直角△ACF中,∠AFC=90°-∠CAF,
直角△AOE中,∠AOE=90°-∠BAF,
又∵∠CAF=∠BAF,
∴∠AFC=∠AOE,
又∵∠AOE=∠FOC,
∴∠AFC=∠FOC,
∴OC=FC.
直角△AOE中,∠AOE=90°-∠BAF,
又∵∠CAF=∠BAF,
∴∠AFC=∠AOE,
又∵∠AOE=∠FOC,
∴∠AFC=∠FOC,
∴OC=FC.
点评:本题考查了直角三角形的性质以及等腰三角形的判定方法,正确证明∠AFC=∠FOC是关键.

练习册系列答案
相关题目
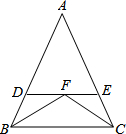 如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )
如图△ABC中,∠B、∠C的角平分线交于点F,过F作DE∥BC交AB于D,交AC于E,下列结论:①△BDF,△ADE都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB+AC;④BF=CF;⑤若∠A=80°,则∠BFC=130°,其中正确的有( )| A、2个 | B、3个 | C、4个 | D、5个 |
抽样调查某班学生的身高为(以160cm为基准,超过得记为正,不足的记为负,单位cm):1、-4、2、
-2.5、-2、1、7、-6、-9,这组数据的众数和中位数分别是( )
-2.5、-2、1、7、-6、-9,这组数据的众数和中位数分别是( )
| A、161,158 |
| B、161,167 |
| C、167,158 |
| D、167,161 |
一组数据:2,4,5,6,x的平均数是4,则这组数的标准差是( )
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指( )
| A、连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次 |
| B、连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次 |
| C、抛掷2n次硬币,恰好有n次“正面朝上” |
| D、抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5 |
 如图,已知四边形ABCD和一点O,O与C重合,求作四边形A′B′C′D′,使它与四边形ABCD关于点O对称.
如图,已知四边形ABCD和一点O,O与C重合,求作四边形A′B′C′D′,使它与四边形ABCD关于点O对称.