题目内容
7.若${2^x}=\frac{1}{8}$,则x=-3;若${x^{-1}}=\frac{1}{10}$,则x=10.分析 根据负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:${2^x}=\frac{1}{8}$=2-3,则x=-3;
若${x^{-1}}=\frac{1}{10}$=10-1,则x=10,
故答案为:-3,10.
点评 本题考查了负整数指数幂,利用负整数指数幂与正整数指数幂互为倒数是解题关键.

练习册系列答案
相关题目
18.下列结论正确的是( )
| A. | 函数y=2x中y随x的减小而增大 | |
| B. | 函数y=-2x中y随x的增大而增大 | |
| C. | 函数y=$\frac{2}{x}$中y随x的增大而减小 | |
| D. | 函数y=-$\frac{2}{x}$中,在每个象限内,y随x的增大而增大 |
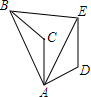 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6.
如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6. 已知,点D是线段AB的黄金分割点,若AD>BD.
已知,点D是线段AB的黄金分割点,若AD>BD.