题目内容
5.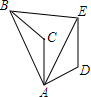 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6.
如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6.
分析 由旋转的性质可知AB=AE=6,∠BAE=60°,从而可证明△ABE是等边三角形,故此可知BE=6.
解答 解:∵由旋转的性质可知:AB=AE=6,∠BAE=60°,
∴△ABE是等边三角形.
∴BE=AB=AE=6.
故答案为:6.
点评 本题主要考查的是旋转的性质、等边三角形的性质和判定,证得三角形ABE为等边三角形是解题的关键.

练习册系列答案
相关题目
20.如果ab>0,bc<0,则函数y=-$\frac{b}{a}$x-$\frac{c}{a}$的图象一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.某公司计划开发制造A、B两种类型的设备共80套,该公司所筹资金不少于2750万元.但不超过2770万元,且所筹资金全部用于制造这两种类型设备.这两种类型设备的制造成本和计划售价如表:
(1)这两种设备可以各制造几套?请求出所有方案.
(2)由于市场变化,公司将每套A型设备的售价提高a万元(a>0),每套B型设备的售价保持不变,若所制造的这两种设备可全部售出,则哪种方案能获得最大利润?(注:利润=售价-成本)
| 类别 | A | B |
| 成本(万元/套) | 30 | 40 |
| 售价(万元/套) | 35 | 47 |
(2)由于市场变化,公司将每套A型设备的售价提高a万元(a>0),每套B型设备的售价保持不变,若所制造的这两种设备可全部售出,则哪种方案能获得最大利润?(注:利润=售价-成本)
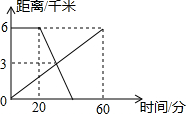 已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知:
已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知: