题目内容
11.已知A(x1,y1)和B(x2,y2)是函数y=$\frac{{k}^{2}+1}{x}$图象上两点,当x1<x2时,y1与y2之间的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
分析 根据反比例函数解析式得到该函数图象经过第一、三象限,结合图象作出判断即可.
解答 解:∵反比例函数y=$\frac{{k}^{2}+1}{x}$中的k2+1>0,
∴该函数图象经过第一、三象限,且在每一象限内y随x的增大而减小.
∴大致图象如图所示: .
.
①当x1<x2<0或0<x1<x2时,y1>y2.
②当x1<0<x2时,y1<y2.
综上所述,无法判断y1与y2之间的大小关系.
故选:D.
点评 本题考查了反比例函数图象上点的坐标特征,解题时,利用了“分类讨论和数形结合”是数学思想.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
1.1.5的倒数是( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
16.$\sqrt{2}$的倒数是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
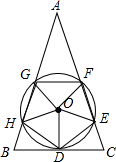 如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.
如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.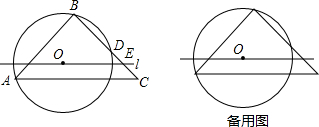
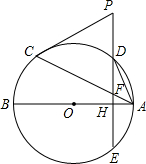 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.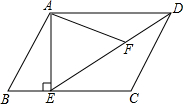 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.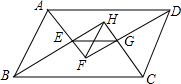 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD与∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.求证:EG=FH.