题目内容
6.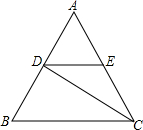 如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.
如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.
分析 由△ABC是等边三角形,CD是∠ACB的平分线,利用三线合一的性质,可得AD=BD,又由DE∥BC,可得DE是△ABC的中位线,即可求得DE的长,易证得△DCE是等腰三角形,则可求得答案.
解答 解:∵△ABC是等边三角形,CD是∠ACB的平分线,
∴AD=BD,∠ACD=∠BCD,
∵DE∥BC,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×3=1.5,∠EDC=∠BCD,
∴∠EDC=∠ACD,
∴EC=DE=$\frac{1}{2}$×3=1.5.
故答案为1.5
点评 本题考查了等边三角形的性质、等腰三角形的判定与性质以及三角形中位线的性质.注意由角平分线与平行线,可构造等腰三角形.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 经过圆心的直线是圆的对称轴 | |
| C. | 和半径垂直的直线是圆的切线 | |
| D. | 三角形的内心到三角形三个顶点距离相等 |
18.一扇形的半径等于已知圆的半径的2倍,且它的面积等于该圆的面积,则这一扇形的圆心角为( )
| A. | 20° | B. | 120° | C. | 100° | D. | 90° |
 如图是2016年巴西奥运会的吉祥物维尼修斯,下列图案中,是通过如图平移得到的图案是( )
如图是2016年巴西奥运会的吉祥物维尼修斯,下列图案中,是通过如图平移得到的图案是( )



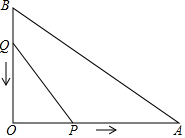 如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么:
如图,在△AOB中,∠AOB=90°,OA=12cm,AB=6$\sqrt{5}$cm,点P从O开始沿OA边向点A以2cm/s(厘米/秒)的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P,Q同时出发,用x(秒)表示时间(0≤x≤6),那么: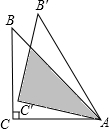 如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.
如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.