题目内容
14.下列说法正确的是( )| A. | 三点确定一个圆 | |
| B. | 经过圆心的直线是圆的对称轴 | |
| C. | 和半径垂直的直线是圆的切线 | |
| D. | 三角形的内心到三角形三个顶点距离相等 |
分析 根据确定圆的条件、三角形内心和外心以及切线的判定定理即可进行判断.
解答 解:A、在同一直线上的三点不能确定一个圆,所以A选项错误;
B、经过圆心的直线是圆的对称轴,所以B选项正确;
C、经过半径的外端点,且垂直于半径的直线是圆的切线,所以C选项错误;
D、三角形的外心到三角形三个顶点距离相等,所以D选项错误.
故选B.
点评 本题考查了确定圆的条件、三角形内心和外心的概念以及切线的判定定理.

练习册系列答案
相关题目
2.某班学生的平均身高是160厘米,表给出了该班6名同学的身高情况(单位:厘米)
(1)完成表:
(2)谁最高?谁最矮?
(3)列式计算最高与最矮的学生身高相差多少?
(1)完成表:
| 姓名 | 小明 | 小彬 | 小丽 | 小亮 | 小颖 | 小山 |
| 身高 | 159 | 161 | 160 | 152 | 162 | 168 |
| 身高与平均身高的差 | -1 | +1 | 0 | -8 | +2 | +8 |
(3)列式计算最高与最矮的学生身高相差多少?
9.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从表可知,
①抛物线与x轴的交点为(-2,0)和(3,0);
②抛物线的对称轴是x=$\frac{1}{2}$;
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$;
④x<$\frac{1}{2}$,y随x增大而增大.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的交点为(-2,0)和(3,0);
②抛物线的对称轴是x=$\frac{1}{2}$;
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$;
④x<$\frac{1}{2}$,y随x增大而增大.
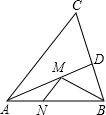 如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.
如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.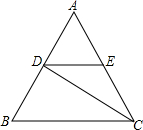 如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5.
如图:△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为3,则EC的长为1.5. 如图,该图形折叠成正方体后,与“沉”字相对的字是考.
如图,该图形折叠成正方体后,与“沉”字相对的字是考.