题目内容
14.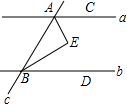 如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )
如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )| A. | 90° | B. | 80° | C. | 60° | D. | 100° |
分析 根据平行线的性质得到∠CAB+∠DBA=180°,根据角平分线的定义得到∠EAB=$\frac{1}{2}∠$CAB,∠ABE=$\frac{1}{2}$∠ABD,根据三角形的内角和即可得到结论.
解答 解:∵a∥b,
∴∠CAB+∠DBA=180°,
∵EA,EB分别平分∠BAC和∠ABD,
∴∠EAB=$\frac{1}{2}∠$CAB,∠ABE=$\frac{1}{2}$∠ABD,
∴∠EAB+∠ABE=$\frac{1}{2}$(∠CAB+∠DBA)=90°,
∴∠E=180°-∠EAB-∠ABE=90°,
故选A.
点评 本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
4. 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
9.设n=$\sqrt{13}$-1,那么n值介于下列哪两数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
13.某市政府为了增强城镇居民抵御大病风险的能力,积极完善城镇居民医疗保险制度,纳入医疗保险的居民大病住院医疗费用的报销比例标准如下表:
设享受医保的某居民一年的大病住院医疗费用为x元,按上述标准报销的金额为y元.请写出800<x≤3000时,y关于x的函数关系式为y=$\frac{1}{2}$x-400.
| 医疗费用范围 | 报销比例标准 |
| 不超过800元 | 不予报销 |
| 超过800元且不超过3000元的部分 | 50% |
| 超过3000元且不超过5000元的部分 | 60% |
| 超过5000元的部分 | 70% |
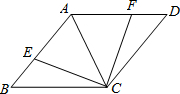 如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.
如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF. 如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
如图,E、F分别是?ABCD的对角线AC上的两点,且CE=AF,求证:BE=DF.
 解下列不等式组,并将它的解集在数轴上表示出来.
解下列不等式组,并将它的解集在数轴上表示出来.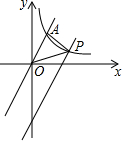 如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.
如图,在平面直角坐标系中,直线y=2x与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=$\frac{k}{x}$在第一象限内的图象交于点P,且△POA的面积为2.