题目内容
19. 如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°,已知测角仪的高度为1.3米.
如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°,已知测角仪的高度为1.3米.(1)求∠BPC的度数;
(2)求该铁塔PC的高度.(结果精确到0.1m;参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
分析 (1)延长PC交直线AB于点G,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BCE中利用三角函数求得CE的长,则PC的长度即可求解.
解答 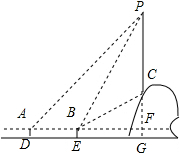 解:(1)延长PC交直线AB于点F,交直线DE于点G,则PF⊥AF,
解:(1)延长PC交直线AB于点F,交直线DE于点G,则PF⊥AF,
依题意得:∠PAF=45°,∠PBF=60°,∠CBF=30°
∴∠BPC=90°-60°=30°;
(2)根据题意得:AB=DE=9,FG=AD=1.3,
设PC=x m,则CB=CP=x,
在Rt△CBF中,BF=x•cos30°=$\frac{\sqrt{3}}{2}$x,CF=$\frac{1}{2}$x,
在Rt△APF中,FA=FP,
∴9+$\frac{\sqrt{3}}{2}$x=$\frac{1}{2}$x+x,x=$9+3\sqrt{3}$,
∴PC=$9+3\sqrt{3}$≈14.2,
即该铁塔PC的高度约为14.2 m.
点评 本题考查了仰角的定义、解直角三角形、三角函数;运用三角函数求出PE和QE是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
11.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
8.如果关于x的不等式2x-a≤0的正整数解是1,2,3,4,那么a的取值范围是( )
| A. | a≥8 | B. | a<10 | C. | 8≤a≤10 | D. | 8≤a<10 |
 如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;
如图.某大街水平地画有两路灯灯秆AB=CD=10米,小明晚上站在两灯杆的正中位置观察眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知底面到小明眼睛处的高度EF=1.5米;