题目内容
3.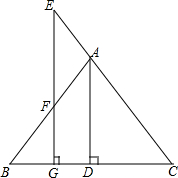 已知:如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AD是∠BAC的角平分线,试说明∠E=∠EFA.
已知:如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AD是∠BAC的角平分线,试说明∠E=∠EFA.
分析 由AD⊥BC,EG⊥BC,由垂直的定义可得∠ADC=∠EGC=90°,由平行线的判定可得AD∥EG,由平行线的性质可得∠E=∠CAD,∠BAD=∠EFA,又因为AD是∠BAC的角平分线,所以∠BAD=∠CAD,等量代换可得结论.
解答 证明:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°,
∴AD∥EG,
∴∠E=∠CAD,∠BAD=∠EFA,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
∴∠E=∠EFA.
点评 本题主要考查了平行线的性质和判定,综合运用平行线的性质和判定定理是解答此题的关键.

练习册系列答案
相关题目
15.下列命题不正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 平移前后图形的形状和大小都没有发生改变 | |
| C. | 两条平行线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,过直线外一点有且只有一条直线与该直线平行 |
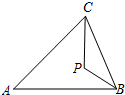 如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC=110°.
如图,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC=110°. 如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.
如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.