题目内容
13. 如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.
如图,∠AOB=90°,C、D是$\widehat{AB}$的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.
分析 连接AC,根据题意证明AE=AC,由AC=CD得到答案.
解答  证明:连接AC,
证明:连接AC,
∵∠AOB=90°,C、D是$\widehat{AB}$的三等分点,
∴∠AOC=∠COD=30°,
∴AC=CD,又OA=OC,
∴∠ACE=75°,
∵∠AOB=90°,OA=OB,
∴∠OAB=45°,
∠AEC=∠AOC+∠OAB=75°,
∴∠ACE=∠AEC,
∴AE=AC,
∴AE=CD.
点评 本题考查的是圆心角、弧、弦的关系,灵活运用三角形内角和定理和三角形外角的性质是解题的关键,注意等量代换的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若二次函数y=ax2+bx+c(a≠0)与x轴交于两个不同点A(x1,0),B(x2,0);且二次函数化为顶点式是y=a(x-h)2+k,则下列说法:
①b2-4ac>0;
②x1+x2=2h;
③二次函数y=ax2+bx+2c(a≠0)化为顶点式为y=a(x-h)2+2k;
④若c=k,则一定有h=b.
正确的有( )
①b2-4ac>0;
②x1+x2=2h;
③二次函数y=ax2+bx+2c(a≠0)化为顶点式为y=a(x-h)2+2k;
④若c=k,则一定有h=b.
正确的有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
8.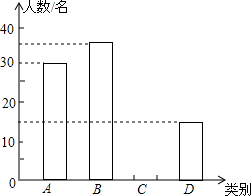 由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
(1)表格中a=30,b=15,并补全条形统计图;
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名?
 由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:
由于各地雾霾天气越来越严重,2015年春节前夕,蚌埠市某校团委向全校3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:不会减少烟花爆竹数量;D类:使用电子鞭炮”四个选项对100名学生进行问卷调查,并将调查结果绘制成如下两幅统计图表(不完整),请根据图表,回答下列问题:| 类别 | 频数 | 频率 |
| A | a | m |
| B | 35 | 0.35 |
| C | 20 | 0.20 |
| D | b | n |
| 合计 | 100 | 1.00 |
(2)如果绘制扇形统计图,请求出C类所占的圆心角的度数;
(3)根据抽样结果,请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名?
18.由若干个相同的小立方体搭成的几何体的三视图如图所示,则组成该几何体的小立方体有( )


| A. | 3块 | B. | 4块 | C. | 5块 | D. | 6块 |
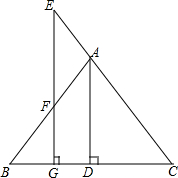 已知:如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AD是∠BAC的角平分线,试说明∠E=∠EFA.
已知:如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AD是∠BAC的角平分线,试说明∠E=∠EFA.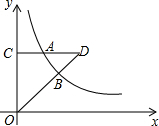 如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12.
如图,A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上两点,AC⊥y轴于C,CA交OB于D,已知$\frac{BD}{OB}$=$\frac{1}{2}$,S四边形OBAC=11,则k=12. 已知,如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE切⊙O于点D,且DE⊥MN于点E.
已知,如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE切⊙O于点D,且DE⊥MN于点E.