题目内容
17.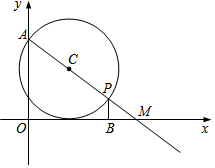 在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=A.
在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=A.(1)AM=10;
(2)如图,以AP为直径作圆,圆心为点C.若⊙C与x轴相切,求A的值;
(3)D是x轴上一点,连接AD、PD.若△OAD∽△BDP,试探究满足条件的点D的个数(直接写出点D的个数及相应A的取值范围,不必说明理由).
分析 (1)直接利用勾股定理计算AM的长;
(2)作CQ⊥x轴于Q,如图,利用切线的性质得CQ=$\frac{1}{2}$AP=a,再证明△CQM∽△AOM,然后利用相似比可计算出a的值;
(3)利用△OAD∽△BDP得到∠OAD=∠BDP,则可证明∠ADP=90°,于是根据圆周角定理的推论可判断点D在以AP为直径的圆上,利用(2)问的结论讨论:当0<a<$\frac{15}{2}$时,⊙C与x轴相离,没有公共点;当a=$\frac{15}{2}$时,⊙C与x轴相切,只有一个公共点,;当a>$\frac{15}{2}$且a≠10时,⊙C与x轴相交,有2个公共点.
解答 解::(1)∵A点坐标是(0,6),M点坐标是(8,0),
∴OA=6,OM=8,
∴AM=$\sqrt{{6}^{2}+{8}^{2}}$=10;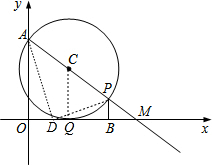
故答案为10;
(2)作CQ⊥x轴于Q,如图,
∵⊙C与x轴相切,
∴CQ=$\frac{1}{2}$AP=a,
∵CQ∥AO,
∴△CQM∽△AOM,
∴$\frac{CQ}{AO}$=$\frac{MC}{MA}$,即$\frac{\frac{1}{2}a}{6}$=$\frac{10-\frac{1}{2}a}{10}$,解得a=$\frac{15}{2}$;
(3)∵△OAD∽△BDP,
∴∠OAD=∠BDP,
而∠OAD+∠ADO=90°,
∴∠ADO+∠BDP=90°,
∴∠ADP=90°,
∴点D在以AP为直径的圆上,
当0<a<$\frac{15}{2}$时,⊙C与x轴相离,没有公共点,所以满足条件的D点有0个;
当a=$\frac{15}{2}$时,⊙C与x轴相切,只有一个公共点,所以没满足条件的D点有1个;
当a>$\frac{15}{2}$且a≠10时,⊙C与x轴相交,有2个公共点,所以满足条件的D点有2个.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、切线的性质和直线与圆的位置关系;会利用相似三角形的知识和勾股定理计算线段的长.理解坐标与图形的性质.

 阅读快车系列答案
阅读快车系列答案| A. | x<-1 | B. | x>-1 | C. | x<1 | D. | x>1 |
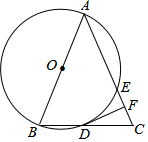 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.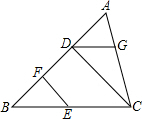 已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.
已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.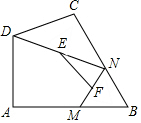 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )