题目内容
6.如果方程kx2+2x+1=0有实数根,则实数k的取值范围是k≤1.分析 分二次项系数k=0和k≠0两种情况考虑:当k=0时,解一元一次方程可求出x的值,由此得出k=0符合题意;当k≠0时,利用根的判别式△≥0即可求出k的取值范围.综上所述即可得出结论.
解答 解:当k=0时,原方程为2x+1=0,
解得:x=-$\frac{1}{2}$,
∴k=0符合题意;
当k≠0时,∵方程kx2+2x+1=0有实数根,
∴△=4-4k≥0,
解得:k≤1且k≠0.
∴实数k的取值范围是k≤1.
故答案为:k≤1.
点评 本题考查了根的判别式、解一元一次方程以及解一元一次不等式,分二次项系数k=0和k≠0两种情况考虑是解题的关键.

练习册系列答案
相关题目
17.计算$\sqrt{2}$•tan 60°的值等于( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
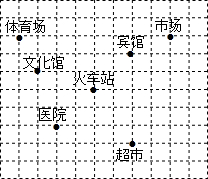 如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2).
如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2). 如图是由4个大小相同的正方体组合而成的几何体,其左视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其左视图是( )



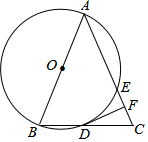 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.