题目内容
11.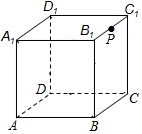 如图,有一个棱长为2cm的正方体,点P为B1C1中点,在A点的一只蚂蚁想吃到P点的食物,则它爬行的最短路程为$\sqrt{13}$cm.
如图,有一个棱长为2cm的正方体,点P为B1C1中点,在A点的一只蚂蚁想吃到P点的食物,则它爬行的最短路程为$\sqrt{13}$cm.
分析 正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短,根据勾股定理可求出路径长,
解答 解:有两种情况:
当展成的长方形:长为2+1=3,宽为2时,最短路径为:$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
当展成的长方形:长为2+2=4,宽为1时,最短路径为:$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$.
故蚂蚁爬行的最短路径长为$\sqrt{13}$cm.
故答案为:$\sqrt{13}$.
点评 本题考查平面展开最短路径问题,关键是知道两点之间线段最短,找到起点终点,根据勾股定理求出,关键是有两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.把根号外的因式化到根号内:-a$\sqrt{-a}$=( )
| A. | $\sqrt{-{a}^{2}}$ | B. | $\sqrt{-{a}^{3}}$ | C. | -$\sqrt{-{a}^{3}}$ | D. | $\sqrt{{a}^{3}}$ |
2.下列变形错误的是( )
| A. | 若-$\frac{1}{2}$x=6,则x=-12 | B. | 若3x=x+1,则2x=1 | ||
| C. | 若x2=y2,则x=y | D. | 若x=y,则x2=y2 |
6.下列方程中,是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=1 | B. | x2+3x-1=0 | C. | ax2+bx+c | D. | 3x+y=10 |
16. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )| A. | 60° | B. | 80° | C. | 40° | D. | 50° |