题目内容

16．如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的度数等于（　　）
A．60°B．80°C．40°D．50°

分析 由OB=OC，∠OCB=40°，根据等边对等角与三角形内角和定理，即可求得∠BOC的度数，又由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，求得∠A的度数．

解答 解：∵OB=OC，∠OCB=40°，
∴∠OBC=∠OCB=40°，
∴∠BOC=180°-40°-40°=100°，
∴∠A=$\frac{1}{2}$∠BOC=50°．
故选D．

点评 此题考查了圆周角定理与等腰三角形的性质．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．

练习册系列答案
相关题目
6．在△ABC中，AB、BC的垂直平分线相交于三角形内一点O，下列结论中，错误的是（　　）
A．点O在AC的垂直平分线上B．△AOB、△BOC、△COA都是等腰三角形
C．∠OAB+∠OBC+∠OCA=90°D．点O到AB、BC、CA的距离相等
7．抛物线y=ax2+bx-4与x轴交于A、B两点，（点B在点A的右侧）且A、B两点的坐标分为（-2，0）、（8，0），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，使其对角线在坐标轴上，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线L交抛物线于点Q．
（1）求抛物线的解析式；
（2）试问抛物线上是否存在点N（不同于点C），使△OEN的面积等于△BOC的面积？若存在，请求出点N的坐标；若不存在，请说明理由；
（3）当点P在线段OB上运动时，直线l交BD于点M．试探究m为何值时，四边形CQMD是平行四边形，并说明理由．
4．解下列方程：
（1）x2-6x=0；   
（2）2（x-3）2=x2-9．
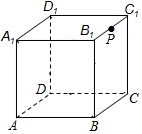11．如图，有一个棱长为2cm的正方体，点P为B1C1中点，在A点的一只蚂蚁想吃到P点的食物，则它爬行的最短路程为$\sqrt{13}$cm．
1．已知：如图，在平面直角坐标系中，点A、C在y轴正半轴上，点B在 x轴负半轴上，且AO=OB=m，OC=n，满足m2-12m+36+（n-4）2=0．点P从点O出发，以每秒2个单位的速度沿x轴正半轴运动，设点P的运动时间为t秒．求：
（1）填空m=6，n=4；
（2）在点P的运动过程中，过点B作直线AP的垂线，交y轴于F，设△PCF的面积为S，请用含t的式子表示出S，并直接写出t的取值范围；
（3）在点P的运动过程中，过点A作直线l，且l∥x轴，直线l上是否存在点Q，使△CPQ是等腰直角三角形？若存在，求出符合条件的t值，若不存在，说明理由．
8．已知长方形纸片的长为31.4厘米，宽为5厘米，用它围成一个高为5厘米的圆柱体，求圆柱的一个底面的面积．（π取3.14）
5．已知单项式3x3yn与-4xmy2是同类项，则m-n2=-1．
6．点M（x，y）在第四象限，且|x|=2，y2=4，则点M的坐标是（　　）
A．（2，2）B．（-2，-2）C．（2，-2）D．（-2，2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网