题目内容
请阅读下列材料:
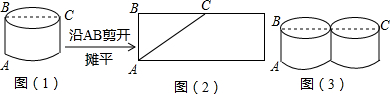
实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l2=AB+BC=5+10=15,l22=225.
为比较l1,l2的大小,我们采用如下方法:
∵l12-l22=25+25π2-225=25π2-200=25(π2-8)>0.
∴l12>l22,所以l1>l2,
小明认为应选择路线2较短.
(1)问题类比:
小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2= ;
路线2:l2=AB+BC= ,l22= .
∵l12 l22,∴l1 l2(填“>”或“<”)
∴小亮认为应选择路线 (填1或2)较短.
(2)问题拓展:
请你帮小明和小亮继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,
路线1:l12= ;
路线2:l22= .
当
满足什么条件时,选择的路2最短?请说明理由.
(3)问题解决:
如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当圆柱的底面半径r(厘米)= 时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条线段相等(注:按上面小明所设计的两条路线方式).
实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l2=AB+BC=5+10=15,l22=225.
为比较l1,l2的大小,我们采用如下方法:
∵l12-l22=25+25π2-225=25π2-200=25(π2-8)>0.
∴l12>l22,所以l1>l2,
小明认为应选择路线2较短.
(1)问题类比:
小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2=
路线2:l2=AB+BC=
∵l12
∴小亮认为应选择路线
(2)问题拓展:
请你帮小明和小亮继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,
路线1:l12=
路线2:l22=
当
| r |
| h |
(3)问题解决:
如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当圆柱的底面半径r(厘米)=

考点:平面展开-最短路径问题
专题:
分析:(1)由阅读材料,可知路线1:l12=AC2=AB2+BC2=高2+底面周长一半2;路线2:l22=(高线AB+底面直径BC)2;将数据代入即可求出l12、l22的值,再运用差比法即可得出l1<l2;
(2)先根据阅读材料用含h、r的代数式分别表示l12、l22,再由l12>l22列出关于h、r的不等式,解不等式即可求解;
(3)先根据阅读材料将h=5代入,用含r的代数式分别表示l12、l22,再由l12=l22列出关于r的方程,解方程即可.
(2)先根据阅读材料用含h、r的代数式分别表示l12、l22,再由l12>l22列出关于h、r的不等式,解不等式即可求解;
(3)先根据阅读材料将h=5代入,用含r的代数式分别表示l12、l22,再由l12=l22列出关于r的方程,解方程即可.
解答:解:(1)如图(2).
∵圆柱的底面半径为1厘米,高AB为5厘米,
∴路线1:l12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+BC=5+2=7,l22=(AB+BC)2=49.
∵l12-l22=25+π2-49=π2-24<0,
∴l12<l22,
∴l1<l2,
∴选择路线1较短;
 (2)如图(2).
(2)如图(2).
∵圆柱的底面半径为r厘米,高为h厘米,
∴路线1:l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2,
路线2:l22=(AB+BC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h];
∵r恒大于0,
∴当(π2-4)r-4h>0,即
>
时,l12>l22,即此时选择的路2最短;
(3)如图(3),圆柱的高为5厘米.
l12=AC2=AB2+BC2=25+(2πr)2,
l22=(AB+BC)2=(5+4r)2,
由题意,得25+(2πr)2=(5+4r)2,
解得r=
.
即当圆柱的底面半径r为
厘米时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条线段相等.
故答案为:25+π2,7,49,<,<1;h2+π2r2,(h+2r)2;
.
∵圆柱的底面半径为1厘米,高AB为5厘米,
∴路线1:l12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+BC=5+2=7,l22=(AB+BC)2=49.
∵l12-l22=25+π2-49=π2-24<0,
∴l12<l22,
∴l1<l2,
∴选择路线1较短;
 (2)如图(2).
(2)如图(2).∵圆柱的底面半径为r厘米,高为h厘米,
∴路线1:l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2,
路线2:l22=(AB+BC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h];
∵r恒大于0,
∴当(π2-4)r-4h>0,即
| r |
| h |
| 4 |
| π2-4 |
(3)如图(3),圆柱的高为5厘米.
l12=AC2=AB2+BC2=25+(2πr)2,
l22=(AB+BC)2=(5+4r)2,
由题意,得25+(2πr)2=(5+4r)2,
解得r=
| 10 |
| π2-4 |
即当圆柱的底面半径r为
| 10 |
| π2-4 |
故答案为:25+π2,7,49,<,<1;h2+π2r2,(h+2r)2;
| 10 |
| π2-4 |
点评:本题考查了平面展开-最短路径问题,比较两个式子的大小,通常利用差比法,这里让这两个式子的平方相减.同时考查了学生的阅读理解能力,知识的迁移能力及分析问题解决问题的能力.

练习册系列答案
相关题目
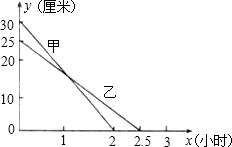 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示.
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示. 某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示.
某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示. 如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=
如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=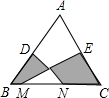 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为 如图,PA、PB切⊙O于A、B,D是弧AB上任一点,过点D作⊙O的切线交PA、PB于点E、F.
如图,PA、PB切⊙O于A、B,D是弧AB上任一点,过点D作⊙O的切线交PA、PB于点E、F. 现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件:
现有一个顶角为36°的等腰三角形,将其分割成4个等腰三角形(根据要求画出图形,标出底角度数),4个等腰三角形满足如下各自条件: