题目内容
 如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=
如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=考点:平行线分线段成比例
专题:
分析:作DF∥BE交AC于F,由D是BC的中点根据平行线等分线段定理可以得出F是EC的中点,就可以表示出EF的长度,再根据相似三角形的性质就可以得出结论.
解答: 解:作DF∥BE交AC于F,
解:作DF∥BE交AC于F,
∵AD是△ABC的中线,
∴EF=FC=
EC,
∵AE:EC=1:3,设AE=x,EC=3x,
∴EF=1.5x.
∵DF∥BE,
∴△AGE∽△ADF,
∴
=
,
∴
=
,
∴
=
.
故答案为:2:3.
 解:作DF∥BE交AC于F,
解:作DF∥BE交AC于F,∵AD是△ABC的中线,
∴EF=FC=
| 1 |
| 2 |
∵AE:EC=1:3,设AE=x,EC=3x,
∴EF=1.5x.
∵DF∥BE,
∴△AGE∽△ADF,
∴
| AG |
| GD |
| AE |
| EF |
∴
| AG |
| GD |
| x |
| 1.5x |
∴
| AG |
| GD |
| 2 |
| 3 |
故答案为:2:3.
点评:本题考查了平行线分线段成比例定理的运用,相似三角形的判定与性质的运用,在解答时利用作平行线制造相似三角形是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
在直线、圆、正方形、正五角星、平行四边形中,你认为既是中心对称图形又是轴对称图形的有( )个.
| A、5 | B、4 | C、3 | D、2 |
 如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=
如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列运算正确的是( )
| A、2x+3y=6xy | ||||
| B、(3.14-π)0=0 | ||||
| C、2-1=-2 | ||||
D、(
|
 如图,C是
如图,C是
 已知:如图,在△ABC中,D是AB上一点,E是AC上一点,且∠AED=∠ABC.
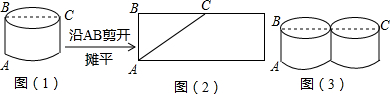
已知:如图,在△ABC中,D是AB上一点,E是AC上一点,且∠AED=∠ABC. 如图1所示,以此图右边缘所在直线为轴将图形向右翻转180°后,再将所得到的图形绕其中心按顺时针方向旋转180°所得到的图形是( )
如图1所示,以此图右边缘所在直线为轴将图形向右翻转180°后,再将所得到的图形绕其中心按顺时针方向旋转180°所得到的图形是( )



 如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为( )
如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为( )