题目内容
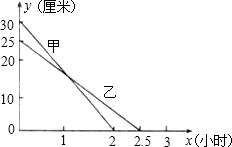在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（厘米）与燃烧时间X（小时）之间的关系如图所示．（1）甲、乙两根燃烧的高度分别是
（2）分别求出甲、乙两根蜡烛燃烧时，y与x之间的函数关系式．
（3）燃烧多长时间，甲、乙两根蜡烛燃烧的高度相等（不考虑都燃尽时的情况）
考点：一次函数的应用
专题：
分析：（1）通过观察图象可以直接得出甲、乙两根燃烧的高度及从点燃到燃尽的时间；
（2）设y甲=k1x+b1，y乙=k2x+b2，根据待定系数法可以直接求出结论．
（3）当y甲=y乙时，建立一个一元一次方程就可以求出其解．
（2）设y甲=k1x+b1，y乙=k2x+b2，根据待定系数法可以直接求出结论．
（3）当y甲=y乙时，建立一个一元一次方程就可以求出其解．
解答：解：（1）根据题意和图象得：
甲、乙两根燃烧的高度分别是30cm，25cm；
从点燃到燃尽的时间分别是2小时，2.5小时；
故答案为：30cm，25cm；2小时，2.5小时．
（2）设y甲=k1x+b1，y乙=k2x+b2，由图象得
，
，
解得：
，
，
则y甲=-15x+30，y乙=-10x+25，
（3）当y甲=y乙时，
-15x+30=-10x+25，
x=1，
故燃烧1小时，甲、乙两根蜡烛燃烧的高度相等．
甲、乙两根燃烧的高度分别是30cm，25cm；
从点燃到燃尽的时间分别是2小时，2.5小时；
故答案为：30cm，25cm；2小时，2.5小时．
（2）设y甲=k1x+b1，y乙=k2x+b2，由图象得
|
|
解得：
|
|
则y甲=-15x+30，y乙=-10x+25，
（3）当y甲=y乙时，
-15x+30=-10x+25，
x=1，
故燃烧1小时，甲、乙两根蜡烛燃烧的高度相等．
点评：本题是一道一次函数的综合试题，考查了自变量与函数之间的变化关系，待定系数法求一次函数的解析式的运用及一次函数与一元一次方程的关系，解答时求出函数的解析式是关键．
练习册系列答案
相关题目
=
如图，C是
为了解某班学生每天使用零花钱的情况，小红随机调查了15名同学，结果如下表：
则这15名同学每天使用零花钱的众数和中位数分别是（ ）
| 每天使用零花钱（单位：元） | 3 | 5 | 7 | 10 | 20 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
| A、7，7 | B、5，5 |
| C、7，5 | D、5，7 |
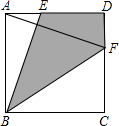如图，E、F分别是正方形ABCD的边AD、DC上的点，BE⊥AF，若图中阴影部分的面积为8，则正方形的面积是（ ）| A、12 | B、16 | C、20 | D、24 |
化简
的结果正确的是（ ）
| 27 |
| A、3 | ||
B、3
| ||
| C、4 | ||
D、2
|
在直线、圆、正方形、正五角星、平行四边形中，你认为既是中心对称图形又是轴对称图形的有（ ）个．
| A、5 | B、4 | C、3 | D、2 |
