题目内容
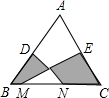 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为考点:相似三角形的判定与性质,三角形的面积,等腰三角形的性质,勾股定理,三角形中位线定理
专题:压轴题
分析:由勾股定理求出BC上的高AN为8cm,求出AO=ON=4cm,求出MN=DE MN∥DE,求出MN与DE间的距离是4cm,求出△MNO和△DEO的高均为cm2,求出阴影部分面积即可.
解答:
解:连接DE,过A作AH⊥BC于H,过O作ZF⊥BC于F,交DE于Z,
∵AB=AC=10cm,AH⊥BC,BC=12cm,
∴BH=CH=6cm,
∵AB=AC=10cm,
由勾股定理得:AH=8cm,
∵D、E分别是AB和AC中点,
∴DE=
BC=6cm,DE∥BC,
∴DE和MN间的距离是4cm,
∵MN=6cm,BC=12cm,
∴MN=DE,MN∥DE,
∴∠DEO=∠NMO,
在△DEO和△NMO中,
∵
,
∴△DEO≌△NMO(AAS),
∴DO=NO,
∵DE∥MN,
∴△DZO∽△NFO,
∴
=
,
∵DO=ON,
∴ZO=OF=
ZF=2cm,
∴阴影部分的面积是:
S梯形DECB-S△DOE-S△OMN
=
×(DE+BC)×FZ-
×DE×OZ-
×MN×OF
=
×(6+12)×4-
×6×2-
×6×2
=24(cm2).
故答案为:24.

解:连接DE,过A作AH⊥BC于H,过O作ZF⊥BC于F,交DE于Z,
∵AB=AC=10cm,AH⊥BC,BC=12cm,
∴BH=CH=6cm,
∵AB=AC=10cm,
由勾股定理得:AH=8cm,
∵D、E分别是AB和AC中点,
∴DE=
| 1 |
| 2 |
∴DE和MN间的距离是4cm,
∵MN=6cm,BC=12cm,
∴MN=DE,MN∥DE,
∴∠DEO=∠NMO,
在△DEO和△NMO中,
∵
|
∴△DEO≌△NMO(AAS),
∴DO=NO,
∵DE∥MN,
∴△DZO∽△NFO,
∴
| DO |
| ON |
| ZO |
| OF |
∵DO=ON,
∴ZO=OF=
| 1 |
| 2 |
∴阴影部分的面积是:
S梯形DECB-S△DOE-S△OMN
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=24(cm2).
故答案为:24.
点评:本题考查了相似三角形的性质和判定,三角形的面积,等腰三角形的性质,勾股定理,三角形的中位线定理等知识点的综合运用.

练习册系列答案
相关题目
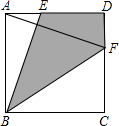 如图,E、F分别是正方形ABCD的边AD、DC上的点,BE⊥AF,若图中阴影部分的面积为8,则正方形的面积是( )
如图,E、F分别是正方形ABCD的边AD、DC上的点,BE⊥AF,若图中阴影部分的面积为8,则正方形的面积是( )| A、12 | B、16 | C、20 | D、24 |
 如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=
如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )
如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )| A、60° | B、70° |
| C、75° | D、80° |
下列运算正确的是( )
| A、2x+3y=6xy | ||||
| B、(3.14-π)0=0 | ||||
| C、2-1=-2 | ||||
D、(
|
 如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF是( )
如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF是( )| A、20000m |
| B、400m |
| C、200m |
| D、199.2m |
 已知:如图,在△ABC中,D是AB上一点,E是AC上一点,且∠AED=∠ABC.
已知:如图,在△ABC中,D是AB上一点,E是AC上一点,且∠AED=∠ABC.