题目内容
1．
作图题：已知：直线a和直线外一点A，过A点作直线a的平行线．
分析 用三角板的一条直角边的已知直线重合，另一条直角边与直尺重合，沿直尺平移三角板，使三角板的与已知直线重合那条直角边和A点重合，过A沿直角边向已知直线画直线即可．
解答 解：根据题意，运用三角板画出过点A的直线，直线b即为所求，
如图所示：
点评 本题考查了平行线的意义、平移、利用三角板和直尺作平行线的方法；熟练掌握平行线的意义是解决问题的关键，通过作图操作利于培养学生的作图能力．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
如图，已知：AB∥DE，AB=DE，∠1=∠2，求证：FC=GC．
12．
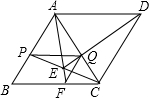如图，在菱形ABCD中，AC=AB，P是AB边上的任意一点（点P与A，B两点不重合），PQ∥BC交AC于点Q，DQ的延长线交PC于点E，AE的延长线交BC于点F，连接FQ，则下列结论错误的是（ ）
如图，在菱形ABCD中，AC=AB，P是AB边上的任意一点（点P与A，B两点不重合），PQ∥BC交AC于点Q，DQ的延长线交PC于点E，AE的延长线交BC于点F，连接FQ，则下列结论错误的是（ ）| A． | FQ∥AB | B． | AQ=BF | ||
| C． | ∠PEF=120° | D． | DE不是∠AEC的平分线 |
9．如图，数轴上有一个质点从原点出发，沿数轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动，质点落在表示数3的点上（允许重复过此点），则质点的不同运动方案共有（ ）
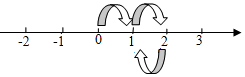
| A． | 2种 | B． | 3种 | C． | 4种 | D． | 5种 |
16．
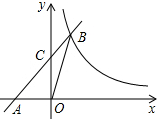直线y=kx+2与x轴交于点A，与y轴交于点C，与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B，连接B0．若S△OBC=1，tan∠BOC=$\frac{1}{3}$，则m的值是（ ）
直线y=kx+2与x轴交于点A，与y轴交于点C，与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B，连接B0．若S△OBC=1，tan∠BOC=$\frac{1}{3}$，则m的值是（ ）| A． | -3 | B． | 1 | C． | ．2 | D． | ．3 |
6．若抛物线y=（a-1）x2-2x+3与x轴有交点，则整数a的最大值是（ ）
| A． | 2 | B． | 1 | C． | 0 | D． | -1 |
13．关于x的二次方程ax2+bx-c=0的两个根是x1=m，x2=n，那么二次函数y=-ax2-bx+c与x轴的两个交点的坐标是（ ）
| A． | （m，0）（n，0） | B． | （m，0）（-n，0） | C． | （-m，0）（n，0） | D． | （-m，0）（-n，0） |