题目内容
4.(1)若一个数的平方根为2a+3和a-9,则这个数是49.(2)若$\sqrt{10}$的整数部分是a,小数部分是b,则${(b-\sqrt{10})^a}$=-27.
分析 (1)根据一个正数的两个平方根互为相反数,可知2a+3+a-9=0,a=2,继而得出答案;
(2)先求得a=3,b=$\sqrt{10}$-3,然后代入计算即可.
解答 解:(1)∵一个正数的两个平方根互为相反数,
∴2a+3+a-9=0.
解得:a=2.
∴2a+3=7.
∴72=49.
∴这个数是49.
故答案为:49.
(2)∵9<10<16,
∴3<$\sqrt{10}$<4.
∴a=3,b=$\sqrt{10}$-3.
∴$(b-\sqrt{10})^{a}$=$(\sqrt{10}-3-\sqrt{10})^{3}$=(-3)3=-27.
故答案为:-27.
点评 本题主要考查的是平方根的定义和性质,求得a、b的值是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
6. 某校为了解2014年七年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2014年七年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数;
(2)该校2014年七年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少
 某校为了解2014年七年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2014年七年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数;
(2)该校2014年七年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少
| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册书(本) | 80 | 80 | m | 48 |
12.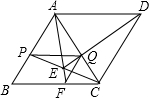 如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )
如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )
 如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )
如图,在菱形ABCD中,AC=AB,P是AB边上的任意一点(点P与A,B两点不重合),PQ∥BC交AC于点Q,DQ的延长线交PC于点E,AE的延长线交BC于点F,连接FQ,则下列结论错误的是( )| A. | FQ∥AB | B. | AQ=BF | ||
| C. | ∠PEF=120° | D. | DE不是∠AEC的平分线 |
9.如图,数轴上有一个质点从原点出发,沿数轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动,质点落在表示数3的点上(允许重复过此点),则质点的不同运动方案共有( )
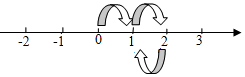

| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
16.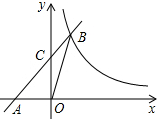 直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
 直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )| A. | -3 | B. | 1 | C. | .2 | D. | .3 |
13.关于x的二次方程ax2+bx-c=0的两个根是x1=m,x2=n,那么二次函数y=-ax2-bx+c与x轴的两个交点的坐标是( )
| A. | (m,0)(n,0) | B. | (m,0)(-n,0) | C. | (-m,0)(n,0) | D. | (-m,0)(-n,0) |
14.点A(-4,y1),B(2,y2)都在直线y=-x-1上,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
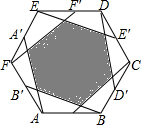 如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.
如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.