题目内容
5. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )
如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且S△ABC=8cm2,则S阴影面积等于( )| A. | 4cm2 | B. | 3cm2 | C. | 2cm2 | D. | 1cm2 |
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵点E是AD的中点,
∴S△ABE=$\frac{1}{2}$S△ABD,S△ACE=$\frac{1}{2}$S△ADC,
∴S△ABE+S△ACE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×8=4,
∴S△BCE=$\frac{1}{2}$S△ABC=4,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×4=2(cm2).
故选C.
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
16.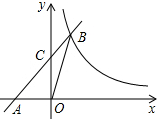 直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
 直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )
直线y=kx+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点B,连接B0.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则m的值是( )| A. | -3 | B. | 1 | C. | .2 | D. | .3 |
13.关于x的二次方程ax2+bx-c=0的两个根是x1=m,x2=n,那么二次函数y=-ax2-bx+c与x轴的两个交点的坐标是( )
| A. | (m,0)(n,0) | B. | (m,0)(-n,0) | C. | (-m,0)(n,0) | D. | (-m,0)(-n,0) |
14.点A(-4,y1),B(2,y2)都在直线y=-x-1上,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
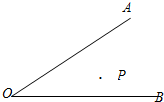 如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,
如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,