题目内容
11.请直接写出$\sqrt{(2m-3)^{2}+1}$+$\sqrt{(8-2m)^{2}+4}$的最小值为$\sqrt{34}$.分析 根据勾股定理得出AC,CE的长进而得出用含x的代数式表示AC+CE的长;由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小,利用勾股定理求出即可.
解答 解:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=5,设CD=2m-3.
∵CD=2m-3,BD=5,
∴CB=8-2m,
AC+CE=$\sqrt{(2m-3)^{2}+1}$+$\sqrt{(8-2m)^{2}+4}$,
A、C、E在同一直线上,AC+CE最小;
当A、C、E在同一直线上时,
延长AB,作EF⊥AB于点F,
∵AB=2,DE=1,
∴AF=3,
∵∠ABD=90°,
∴∠FBD=90°,
∵∠BDE=∠BFE=90°,
∴四边形BFED是矩形,
∴BD=EF=5,
∴AE=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∴$\sqrt{(2m-3)^{2}+1}$+$\sqrt{(8-2m)^{2}+4}$的最小值为$\sqrt{34}$
故答案为:$\sqrt{34}$.
点评 本题主要考查了最短路线问题以及勾股定理应用,利用了数形结合的思想,通过构造直角三角形,利用勾股定理求解是解题关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
2.$\frac{1}{2}$的相反数是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
19.下列各式中能用平方差公式因式分解的是( )
| A. | -x2y2 | B. | x2+y2 | C. | x2-y2 | D. | x-y |
3.如图,小慧用直角曲尺检查半圆形的工件,其中合格的是( )
| A. |  | B. |  | C. |  | D. |  |
1.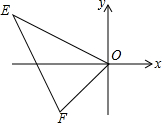 在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )
在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )
 在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )
在平面直角坐标系中,已知点E(-4,2),F(-2,-2).若△OE′F′与△OEF关于点O位似,且S△OE′F′:S△OEF=1:4,则点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,4) | C. | (2,-1) | D. | (8,-4) |
 已知线段a,c的长如图所示,求作Rt△ABC,使斜边AB=c,直角边BC=a.要求用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑.
已知线段a,c的长如图所示,求作Rt△ABC,使斜边AB=c,直角边BC=a.要求用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑. 如图,一艘渔船沿图中所示的折线由A航行到E,问船一共行驶了多少海里?
如图,一艘渔船沿图中所示的折线由A航行到E,问船一共行驶了多少海里?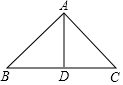 如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.
如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.


