题目内容
16.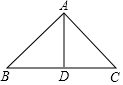 如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.
如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.
分析 由已知条件根据等腰三角形三线合一的性质可得到BD=DC,再根据三角形的周长定义求解.
解答 解:∵AB=AC,AD⊥BC,
∴BD=DC.
∵AB+AC+BC=20,
即AB+BD+CD+AC=20,
∴AC+DC=10,
∴AC+DC+AD=16,
∴AD=6.
故答案为:6.
点评 本题考查等腰三角形的性质;由已知条件结合图形发现并利用AC+CD是△ABC的周长的一半是正确解答本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
4.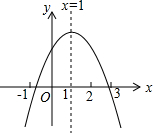 已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
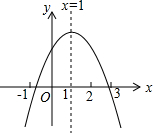 已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k为常数,且k≠1).其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
8.将抛物线y=x2先向右平移1个单位长度,再向下平移2个单位长度可得抛物线( )
| A. | y=(x-1)2-2 | B. | y=(x+1)2-2 | C. | y=(x-1)2+2 | D. | y=(x+1)2+2 |
5.能说明命题“若x(x+1)(x-2)=0,则x=0”是假命题的反例是( )
| A. | x=0 | B. | x=-2 | C. | x=1 | D. | x=-1 |
6.点P(-1,2)关于x轴对称点的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
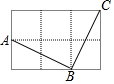 在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
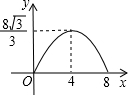
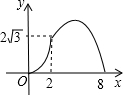
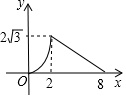
在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.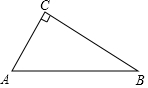 如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )