题目内容
15.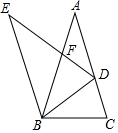 如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.
如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 先根据△ABC与△BED都是顶角为36°的等腰三角形可得出ABC∽△EBD,再由BC2=CD•AC可得出△BCD∽△ABC,∠CBD=∠ABD=∠A=36°,故可得出△BCD∽△EBD;同理,△BDF∽△BCD∽△ABC∽EBD;△ADF∽△EBF∽△ABD.
解答 解:∵△ABC与△BED都是顶角为36°的等腰三角形,
∴ABC∽△EBD.
∵BC2=CD•AC,
∴△BCD∽△ABC,
∴∠CBD=∠ABD=∠A=36°,
∴△BCD∽△EBD;
同理,△BDF∽△BCD∽△ABC∽EBD,△ADF∽△EBF∽△ABD.
故选D.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理与等腰三角形的性质是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
6.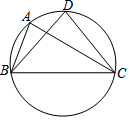 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )| A. | 70° | B. | 50° | C. | 45° | D. | 30° |
10.下列计算正确的是( )
| A. | (-x2)3=-x6 | B. | x4•x2=x8 | C. | (x3)2=-x5 | D. | x3•x2=2x6 |
5.已知菱形的面积是50cm2,一个内角为30°,则这个菱形的边长为( )
| A. | 8cm | B. | 10cm | C. | 12cm | D. | 14cm |
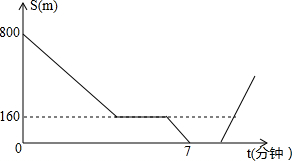 在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.
在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.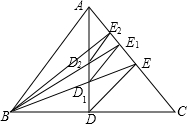 如图,在△ABC中,AB=AC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D;过D1,作D1E1∥AB于E1,连接BE1交AD于D1,过D2作D2E2∥AB于E2,…,如此继续,记S△BDE为S1,S${\;}_{△B{D}_{1}{E}_{1}}$记为S2,S${\;}_{△B{D}_{2}{E}_{2}}$记为S3,…,若S△ABC面积为1,则S2=$\frac{1}{9}$;Sn=$\frac{1}{(n+1)^{2}}$(用含n代数式表示).
如图,在△ABC中,AB=AC,D是边BC的中点,过D作DE∥AB于E,连接BE交AD于D;过D1,作D1E1∥AB于E1,连接BE1交AD于D1,过D2作D2E2∥AB于E2,…,如此继续,记S△BDE为S1,S${\;}_{△B{D}_{1}{E}_{1}}$记为S2,S${\;}_{△B{D}_{2}{E}_{2}}$记为S3,…,若S△ABC面积为1,则S2=$\frac{1}{9}$;Sn=$\frac{1}{(n+1)^{2}}$(用含n代数式表示).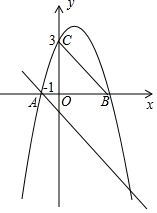 如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.
如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.