题目内容
 如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证:
如图,A,B,C三点在同一直线上,△ADC,△BEC是等边三角形,连接AE,BD.求证:(1)EB∥CD;
(2)AE=DB.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)证明∠ACD=∠EBC,即可解决问题.
(2)证明△ACE≌△DCB,即可解决问题.
(2)证明△ACE≌△DCB,即可解决问题.
解答: 解:(1)证明:∵△ADC,△BEC是等边三角形,
解:(1)证明:∵△ADC,△BEC是等边三角形,
∴∠ACD=60°,∠EBC=60°,
∴∠ACD=∠EBC,
∴EB∥DC.
(2)∵△ADC,△BEC是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE,
∴∠ACE=∠DCB;
在△ACE与△DCB中,
,
∴△ACE≌△DCB(SAS),
∴AE=DB.
 解:(1)证明:∵△ADC,△BEC是等边三角形,
解:(1)证明:∵△ADC,△BEC是等边三角形,∴∠ACD=60°,∠EBC=60°,
∴∠ACD=∠EBC,
∴EB∥DC.
(2)∵△ADC,△BEC是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE,
∴∠ACE=∠DCB;
在△ACE与△DCB中,
|
∴△ACE≌△DCB(SAS),
∴AE=DB.
点评:该题主要考查了全等三角形的判定及其性质、等边三角形的性质等知识点的应用问题;深入观察图形结构特点,准确找出图形中隐含的相等或全等关系是解题的关键.

练习册系列答案
相关题目
 如图,在∠1、∠2、∠3、∠4中,同位角为
如图,在∠1、∠2、∠3、∠4中,同位角为 如图,△ABC内接于⊙O,BC=4,CA=3,∠A-∠B=90°,求⊙O的半径.
如图,△ABC内接于⊙O,BC=4,CA=3,∠A-∠B=90°,求⊙O的半径. 如图,已知等腰△ABC内接于⊙O,AB=AC=5,BC=8,求点O到BC的距离.
如图,已知等腰△ABC内接于⊙O,AB=AC=5,BC=8,求点O到BC的距离. 有长为L的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.
有长为L的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.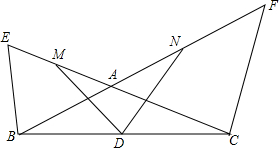 如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点.
如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点. 如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?