题目内容
 如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.(1)试写出△PBQ的面积S与动点运动时间t之间函数表达式;
(2)运动时间t为何值时,△PBQ的面积最大?最大值为多少?
考点:二次函数的应用
专题:几何动点问题
分析:(1)利用两点运动的速度表示出PB,BQ的长,进而表示出△PBQ的面积即可;
(2)利用配方法求出函数顶点坐标即可得出答案.
(2)利用配方法求出函数顶点坐标即可得出答案.
解答:解:(1)由题意得t秒时,PB=(3-t)cm,BQ=2tcm,
S=
PB×BQ=
(3-t)×2t=-t2+3t;
(2)S=-t2+3t=-(t-
)2+
,
故t=
时,S最大=
.
S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)S=-t2+3t=-(t-
| 3 |
| 2 |
| 9 |
| 4 |
故t=
| 3 |
| 2 |
| 9 |
| 4 |
点评:此题主要考查了二次函数的应用,正确表示出PB,BQ的长是解题关键.

练习册系列答案
相关题目
下列各数中,3.14159,
,0.131131113…,-π,
,-
,无理数的个数为( )
| 3 | 8 |
| 16 |
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
有一个角是60°的菱形,它的一条对角线长为6,则这个菱形的边长是( )
| A、6 | ||
| B、3 | ||
C、2
| ||
D、6或2
|
 如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.
如图,在△ABC中,∠BAC=90°,E为AC的中点,AD⊥BC交于D,DE交BA的延长线于F,求证:BF:DF=AB:AC.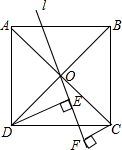 如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明.
如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明. 如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为
如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为