题目内容
有一个角是60°的菱形,它的一条对角线长为6,则这个菱形的边长是( )
| A、6 | ||
| B、3 | ||
C、2
| ||
D、6或2
|
考点:菱形的性质
专题:
分析:作出图形,分①6是较短的对角线时,判断出△ABC是等边三角形,然后根据等边三角形的三条边都相等解答;②6是较长的对角线时,根据菱形的对角线互相垂直平分可得OB=3,菱形的对角线平分一组对角可得∠ABO=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2AO,然后利用勾股定理列方程求解即可.
解答: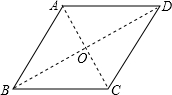 解:如图,①6是较短的对角线时,∵∠ABC=60°,AB=BC,
解:如图,①6是较短的对角线时,∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC=6;
②6是较长的对角线时,∵四边形ABCD是菱形,
∴OB=
×6=3,∠ABO=
∠ABC=
×60°=30°,
∴AB=2AO,
在Rt△ABO中,AB2=BO2+AO2,
即AB2=32+(
AB)2,
解得AB=2
,
综上所述,菱形的边长为6或2
.
故选D.
 解:如图,①6是较短的对角线时,∵∠ABC=60°,AB=BC,
解:如图,①6是较短的对角线时,∵∠ABC=60°,AB=BC,∴△ABC是等边三角形,
∴AB=AC=6;
②6是较长的对角线时,∵四边形ABCD是菱形,
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=2AO,
在Rt△ABO中,AB2=BO2+AO2,
即AB2=32+(
| 1 |
| 2 |
解得AB=2
| 3 |
综上所述,菱形的边长为6或2
| 3 |
故选D.
点评:本题考查了菱形的性质,等边三角形的判定与性质,勾股定理,熟记性质是解题的关键,作出图形更形象直观,难点在于分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
近似数23.16万精确到( )
| A、百分位 | B、百位 | C、千位 | D、万位 |
关于x的一元二次方程(a-1)x2-x+a2-1=0的一个根是0,则a的值为( )
| A、1或-1 | ||
| B、-1 | ||
| C、1 | ||
D、
|
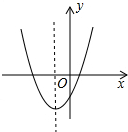 二次函数y=ax2+bx+c的图象如图,点(-
二次函数y=ax2+bx+c的图象如图,点(-| b |
| a |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.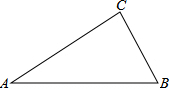 如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.
如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.