题目内容
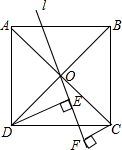 如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明.
如图,一直线l经过正方形ABCD的对角线交点O,过D、C两点作l的垂线,垂足分别为E、F,猜想DE、CF与EF之间的数量关系,并证明.考点:全等三角形的判定与性质,正方形的性质
专题:
分析:易证∠ODE=∠COF,即可求证△COF≌△ODE,即可求得DE=OF,OE=CF,即可解题.
解答:解:∵正方形对角线相等且互相垂直平分,
∴∠COD=90°,OD=OC,
∵∠ODE+∠DOE=90°,∠DOE+∠COF=90°,
∴∠ODE=∠COF,
在△COF和△ODE中,
,
∴△COF≌△ODE(AAS),
∴DE=OF,OE=CF,
∵OF=OE+EF,
∴DE=CF+EF.
∴∠COD=90°,OD=OC,
∵∠ODE+∠DOE=90°,∠DOE+∠COF=90°,
∴∠ODE=∠COF,
在△COF和△ODE中,
|
∴△COF≌△ODE(AAS),
∴DE=OF,OE=CF,
∵OF=OE+EF,
∴DE=CF+EF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△COF≌△ODE是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
据调查,2009年10月湘乡市的房价均价为1500元/m2,2011年10月达到2600元/m2,假设这两年湘乡市房价的平均增长率为x,根据题意可列出方程( )
| A、1500(1+x%)2=2600 |
| B、1500(1+x)2=2600 |
| C、1500(1-x%)2=2600 |
| D、1500(1-x)2=2600 |
 如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4.
如图,以AB为直径的⊙O经过点C,点D为CO延长线上一点,且BC=BD,AB=4. 如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.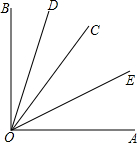 如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.